Question

Помогите пожалуйста номер 20

Answer 1

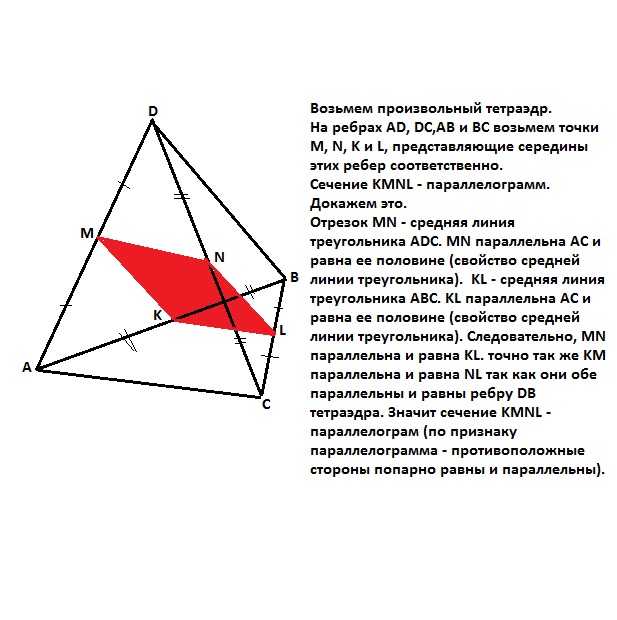
Возьмем произвольный тетраэдр.
На ребрах AD, DC,AB и BC возьмем точки M, N, K и L, представляющие середины этих ребер соответственно.
Сечение KMNL - параллелограмм.
Докажем это.
Отрезок MN - средняя линия треугольника АDC. МN параллельна АС и равна ее половине (свойство средней линии треугольника).  KL - средняя линия треугольника АВС. KL параллельна АС и равна ее половине (свойство средней линии треугольника). Следовательно, MN параллельна и равна KL. точно так же KM параллельна и равна NL так как они обе параллельны и равны ребру DB тетраэдра. Значит сечение KMNL - параллелограм (по признаку параллелограмма - противоположные стороны равны и параллельны).

Answer 2

Andr1806 , добрый вечер . Не могли бы вы помочь с заданием по алгебре ?( логарифмы )