Question

три окружности одинакового радиуса R касаются между собой. между ними вписана окружность радиусом r. нужна формула зависимости r от заданнойR. прошу помочь.

Answer 1

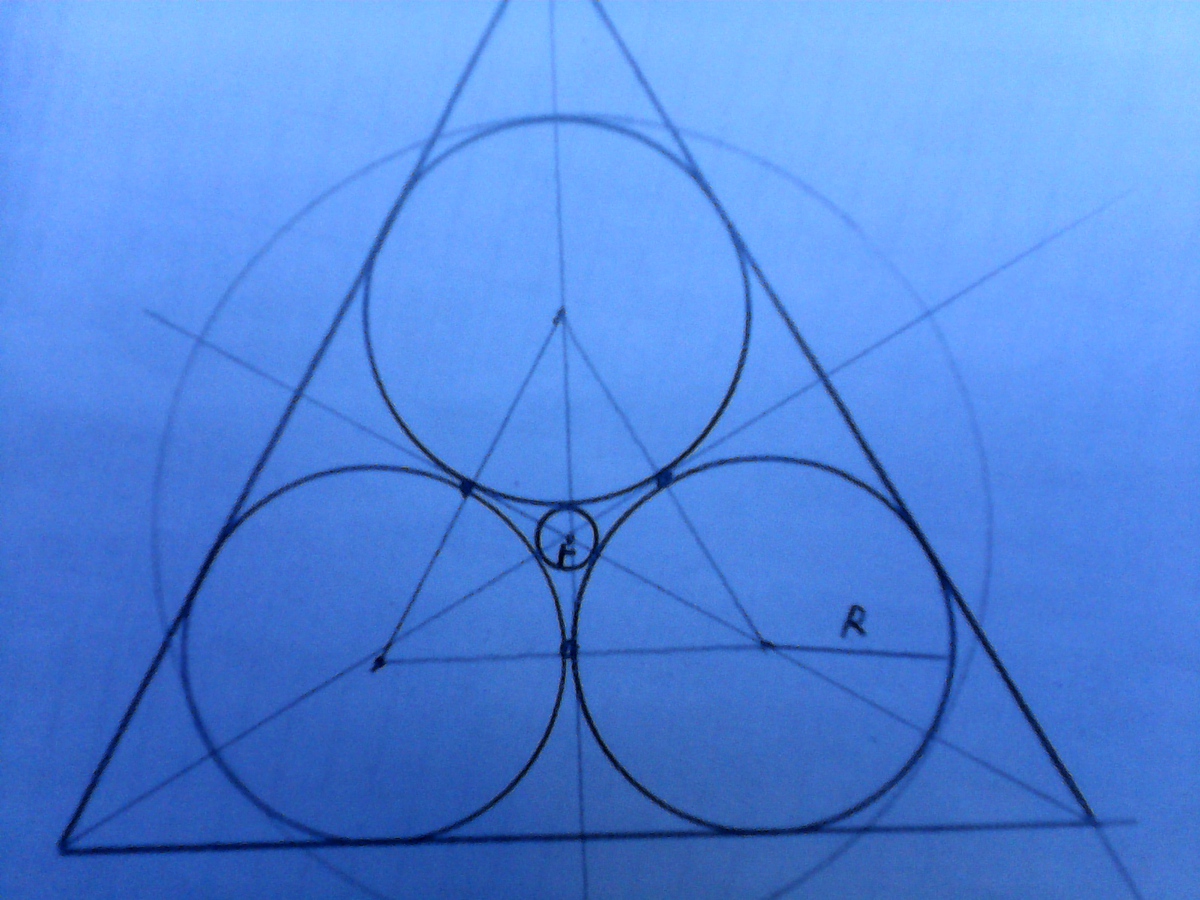
Центр заданной окружности лежит на пересечении биссектрис (они же высоты и медианы) равностороннего треугольника, образованного центрами окружностей радиуса R.
r = (R/cos 30) - R = (R/(√3/2)) - R = (2R/√3) - R = (R*(2-√3)) / √3.