Question

Помогите пожалуйста решить

Answer 1

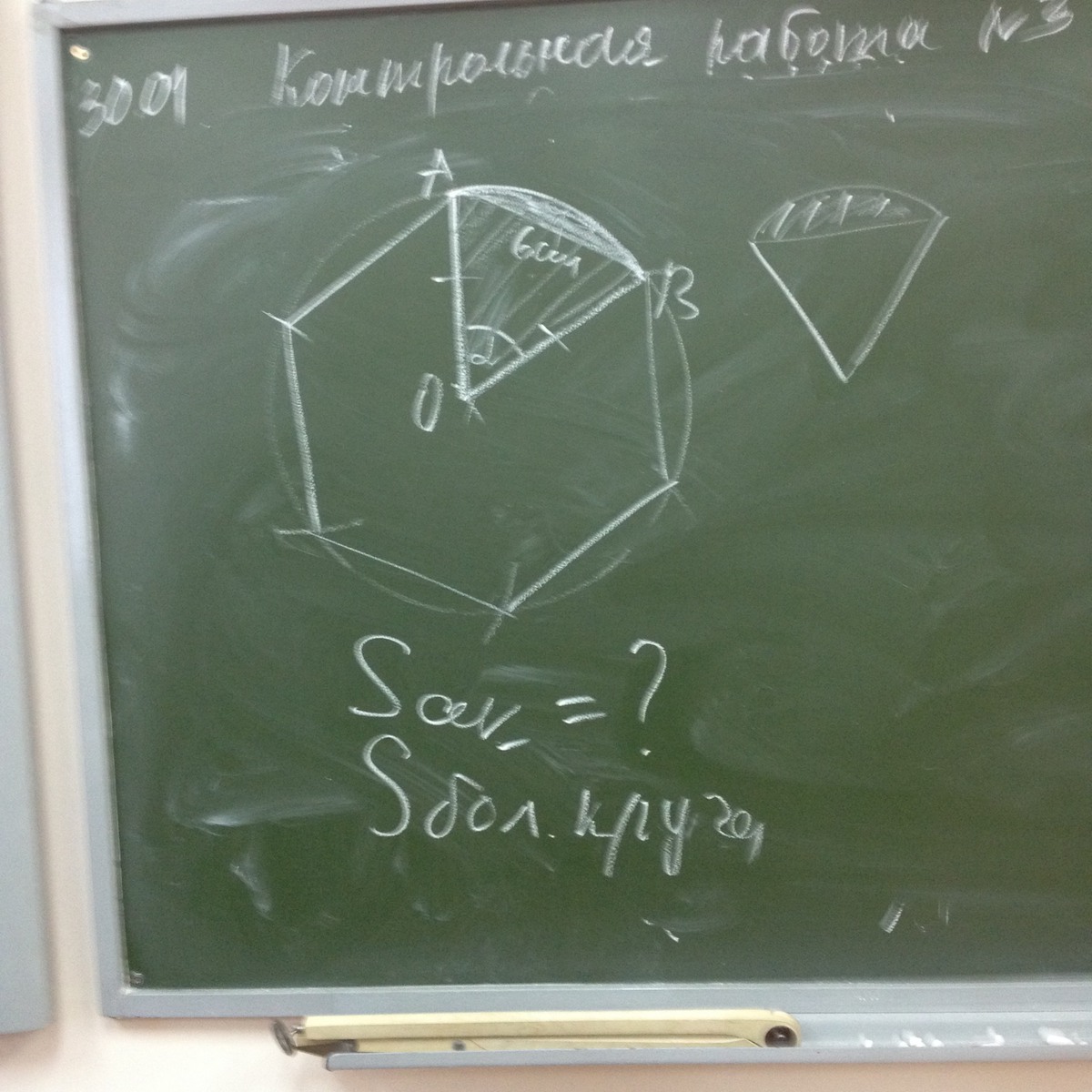
Центральный угол, опирающийся на сторону правильного шестиугольника, вписанного в окружность, равен :
α = 360 / 6 = 60°. Радиус равен стороне R = a = 6 см.
Площадь сектора равна Sск = πR²α/360 = π*6²*60/360 = 6π =  18.84956 см².
Площадь правильного треугольника Sтр = (1/2)а²*sinα = (1/2)*6²*(√3/2) = 9√3 =   15.58846 см².
Площадь сегмента Sсг = Sск - Sтр = 18.84956 - 15.58846 =  3.261099 см².
Площадь круга S = πR² = π*6² = 36π =  113.0973 см².