Найти наименьшее число M, для которого неровность правильная при произвольных значениях числа x.
(укр) Знайти найменше число M, для якого нерівність правильна при довільних значеннях числа x.
Приложения:
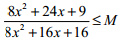
Ответы
Ответ дал:
0
В картинке правильное решение для этой задачи. Сорри, первый раз невнимательно прочитал условие. Также вот еще одно решение, более короткое и хитрое:
 .
.
Максимум этого выражения достигается при x=3 и равен 9/8. Знаменатель всегда положителен, т.к. его дискриминант меньше 0. Т,е. при всех исходное неравенство будет верно при всех
действительных x. Значит минимальное такое М равно 9/8.
исходное неравенство будет верно при всех
действительных x. Значит минимальное такое М равно 9/8.
Максимум этого выражения достигается при x=3 и равен 9/8. Знаменатель всегда положителен, т.к. его дискриминант меньше 0. Т,е. при всех
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад