Ответы
Ответ дал:
0
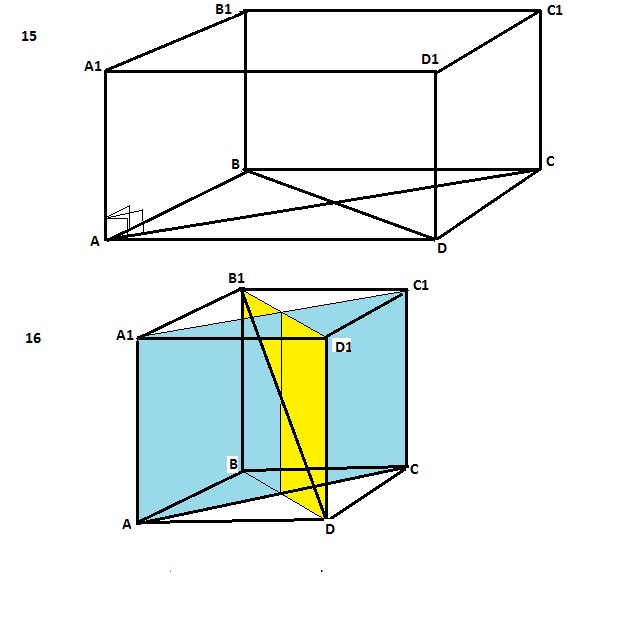
15. Есть теорема: через две пересекающиеся прямые проходит единственная плоскость. Диагонали основания параллелепипеда пересекаются в точке О, значит плоскость АВСD - единственная, солержащая диагонали АС и ВD. Если одно из ребер перпендикулярно диагоналям основания, значит оно перпендикулярно плоскости основания, содержащей эти диагонали. В параллелепипеде боковые грани -параллелограммы, значит их ребра попарно параллельны и, следовательно, перпендикулярны плоскости основания.Параллелепипед, у которого боковые ребра перпендикулярны основанию, является прямым параллелепипедом.
16. В кубе прямые АС и В1D - скрещивающиеся прямые. Проведем плоскость через прямую В1D. Она пройдет и через прямую ВD, являющуюся проекцией прямой В1D на основание АВСD и являющуюся диагональю основания - квадрата. В квадрате диагонали взаимно перпендикулярны.Значит и плоскости АА1С1С и ВВ1D1D взаимно перпендикулярны. Прямая АС принадлежит первой плоскости, а прямая B1D принадлежит второй плоскости, следовательно они также взаимно перпендикулярны.
16. В кубе прямые АС и В1D - скрещивающиеся прямые. Проведем плоскость через прямую В1D. Она пройдет и через прямую ВD, являющуюся проекцией прямой В1D на основание АВСD и являющуюся диагональю основания - квадрата. В квадрате диагонали взаимно перпендикулярны.Значит и плоскости АА1С1С и ВВ1D1D взаимно перпендикулярны. Прямая АС принадлежит первой плоскости, а прямая B1D принадлежит второй плоскости, следовательно они также взаимно перпендикулярны.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
