Ответы
Ответ дал:
0
Вот теоретические знания (фото из учебника)
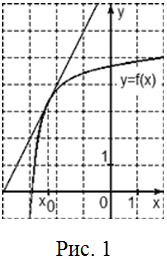
Пример решения. Дан график функции (фото) и касательная к нему в точке с абсциссой икс нулевое. Найти значение производной функции в этой точке.
По определению производная в точке равна отношению приращения функции к приращению аргумента. Выберем на касательной две точки с целочисленными координатами. Пусть, например, это будут точки А(-3;2) и В(-2;4). Найдем приращение аргумента:
Δх=икс второе минус икс первое= -2 - (-3)=-2+3=1
и приращение функции: Δy= игрек второе минус игрек первое = 4-2=2
Тогда окончательно получим,что исковая производная = Δy/Δx=2/1=2
Ответ 2
Пример решения. Дан график функции (фото) и касательная к нему в точке с абсциссой икс нулевое. Найти значение производной функции в этой точке.
По определению производная в точке равна отношению приращения функции к приращению аргумента. Выберем на касательной две точки с целочисленными координатами. Пусть, например, это будут точки А(-3;2) и В(-2;4). Найдем приращение аргумента:
Δх=икс второе минус икс первое= -2 - (-3)=-2+3=1
и приращение функции: Δy= игрек второе минус игрек первое = 4-2=2
Тогда окончательно получим,что исковая производная = Δy/Δx=2/1=2
Ответ 2
Приложения:

Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад