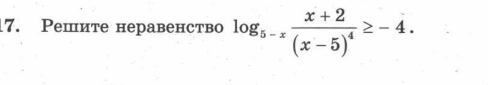Ответы
Ответ дал:
0
Область определения неравенства:
— не удовлетворяет
C учётом
Отбор корней согласно области определения:
Ответ:
Ответ дал:
0
не верно, в ответах второго промежутка нет
Ответ дал:
0
В таком случае отметьте ответ, как нарушение
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад