В треугольнике LKM точка P лежит на стороне LM, причем KP=PM, угол М=40 градусам. Найдите сумму внешних углов при вершине К, если КР -биссектриса угла LKM.
Ответы
Ответ дал:
0
Т. к. КР=РМ, значит треугольник РКМ равнобедренный (КМ-основание), значит угол РКМ равен углу КМР и равен 40 градусам, значит и угол LKP равен 40 градусам, т. к. угол LKP равен углу РКМ (т. к. КР - биссектриса), а следовательно угол LKM равен 40+40=80 градусов, значит внешние углы, смежные с ним, равны 180-80=100 градусов каждый, а значит сумма этих смежных углов равна 100+100=200 градусов.
Ответ: сумма внешних углов при вершине К равна 200 градусам.
Ответ: сумма внешних углов при вершине К равна 200 градусам.
Приложения:
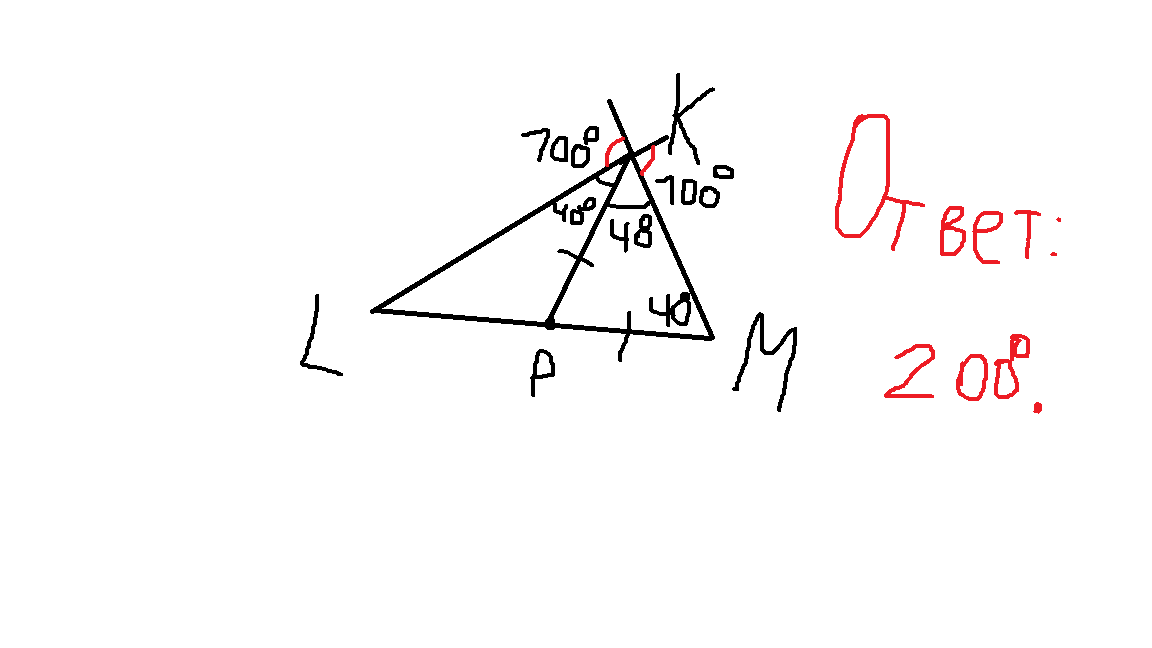
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад