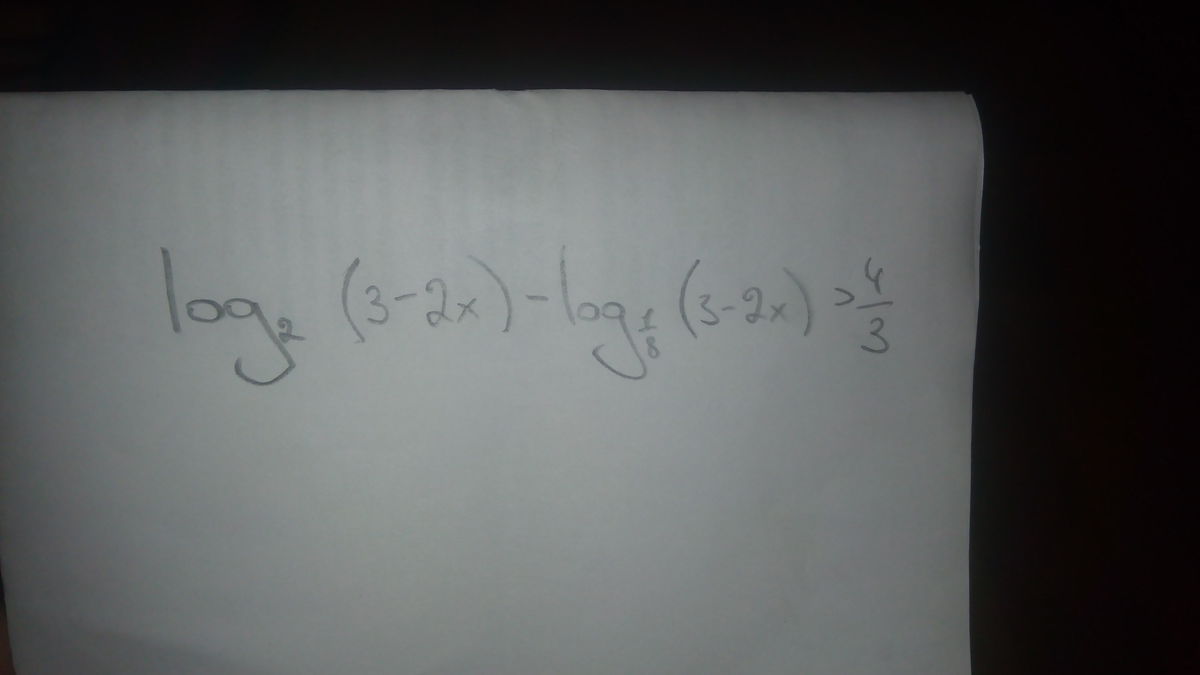Ответы
Ответ дал:
0
Ответ: x∈(-бесконечность; 0.5)
Ответ дал:
0
спасибо большое!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад