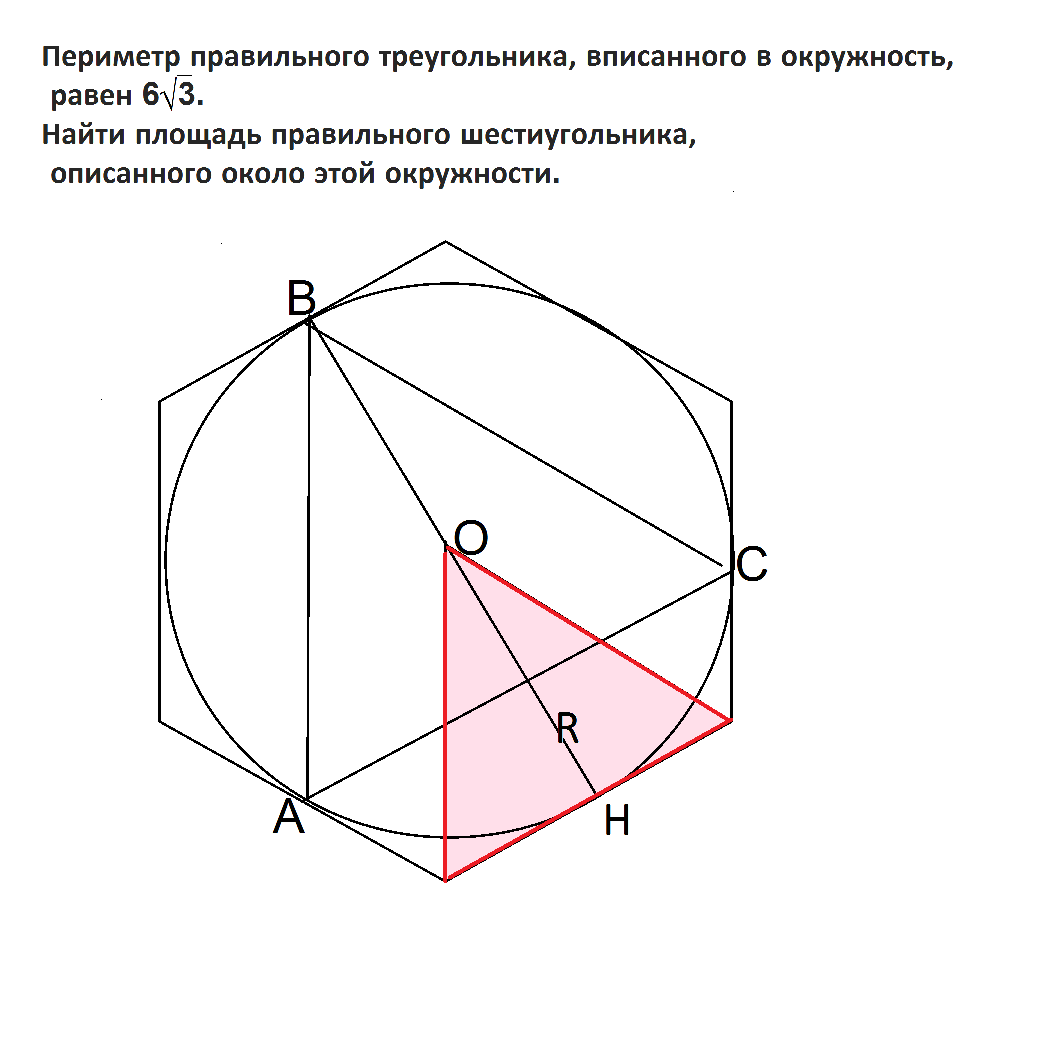
периметр правильного треуг. вписанного в окружность равен 6 корень из 3. найти площадь правильного шестиугольника описанного около этой окружности.
Ответы
Ответ дал:
0
Центр окружности, описанной вокруг правильного треугольника, является и центром окружности, вписанной в правильный шестиугольник.
Радиус R окружности, описанной вокруг правильного треугольника, равен радиусу окружности, вписанной в правильный шестиугольник.
Правильный шестиугольник состоит из 6 равных правильных треугольников, высотой которых является апофема шестиугольника, т.е. радиус вписанной окружности.
Площадь каждого из этих треугольников можно найти по формуле площади правильного треугольника, выраженной через высоту.
S₁=h²/√3,
а площадь всего шестиугольника в 6 раз больше.
Решение:
Сторона а данного треугольника равна
Р:3
а=(6√3):3=2√3
R=a/√3=2
Высота h (апофема шестиугольника) каждого треугольника, из которых состоит правильный шестиугольник, равна ОН - радиусу описанной вокруг правильного треугольника окружности.
Площадь правильного треугольника, выраженная через его высоту
S= h²/√3
S₁=4/√3
S₈=6*4/√3=24/√3
24/√3=(24*√3):(√3*√3)=8√3 (единиц площади)
Радиус R окружности, описанной вокруг правильного треугольника, равен радиусу окружности, вписанной в правильный шестиугольник.
Правильный шестиугольник состоит из 6 равных правильных треугольников, высотой которых является апофема шестиугольника, т.е. радиус вписанной окружности.
Площадь каждого из этих треугольников можно найти по формуле площади правильного треугольника, выраженной через высоту.
S₁=h²/√3,
а площадь всего шестиугольника в 6 раз больше.
Решение:
Сторона а данного треугольника равна
Р:3
а=(6√3):3=2√3
R=a/√3=2
Высота h (апофема шестиугольника) каждого треугольника, из которых состоит правильный шестиугольник, равна ОН - радиусу описанной вокруг правильного треугольника окружности.
Площадь правильного треугольника, выраженная через его высоту
S= h²/√3
S₁=4/√3
S₈=6*4/√3=24/√3
24/√3=(24*√3):(√3*√3)=8√3 (единиц площади)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад