Ответы
Ответ дал:
0
Что не понятно, пишите! объясню!!
Приложения:
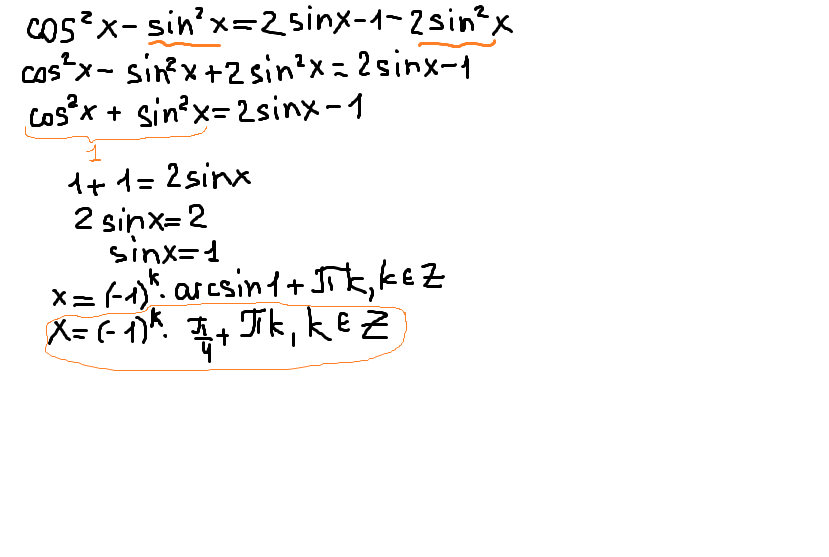
Ответ дал:
0
Приложения:
Вас заинтересует
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад