Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды равно 36. Найдите диаметр окружности
Ответы
Ответ дал:
0
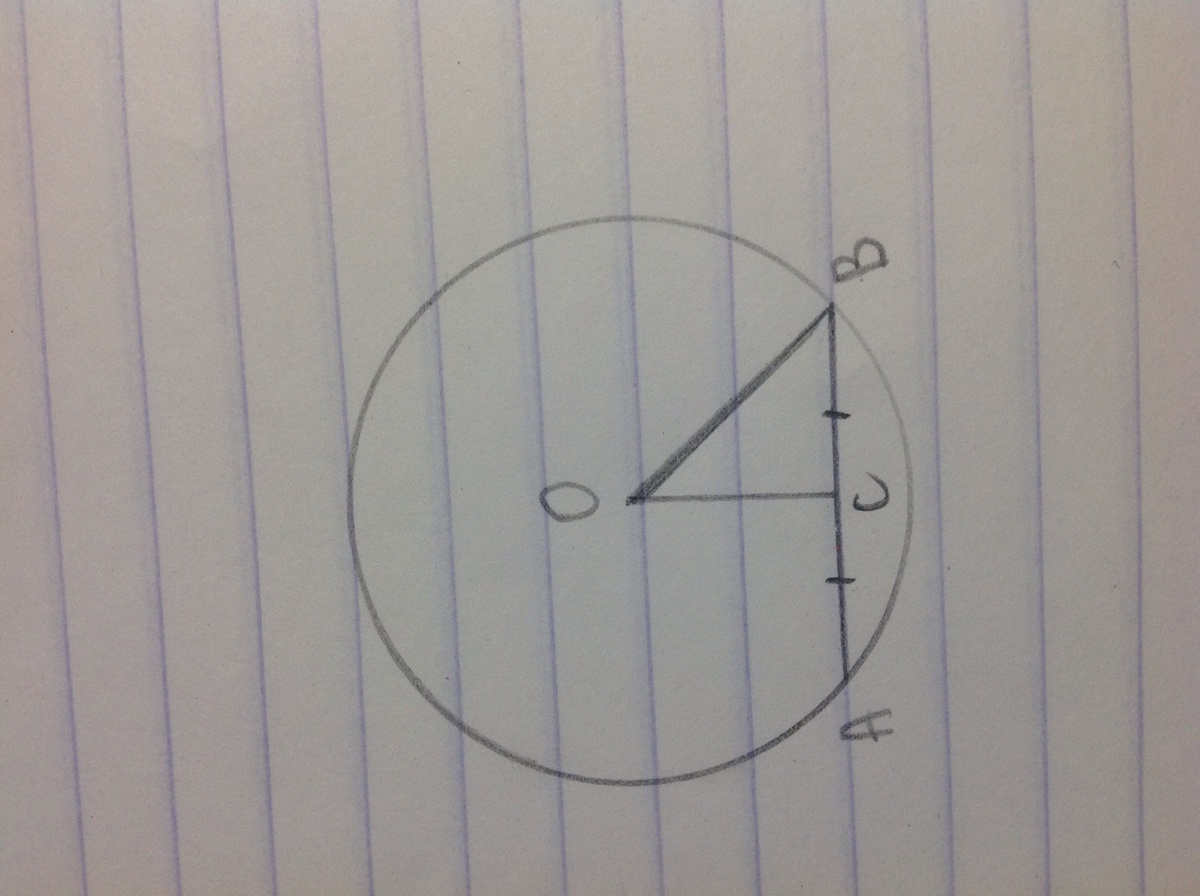
Допустим хорда АВ делится на две равные части точкой С.
Угол ОСВ = 90*.
Сторона ОС (треугольник ОСВ) = 36 (условие).
А сторона СВ = 1/2 АВ = 30:2 = 15
По теореме Пифагора найдем сторону ОВ, которая является радиусом.
ОС в квадрате + СВ в квадрате = ОВ в квадрате
1296+225=1521
ОВ= ОВ=39
D=2R
R=39
D=39*2=78
(Чертеж кривой немного, уж извини)
ОВ=39
D=2R
R=39
D=39*2=78
(Чертеж кривой немного, уж извини)
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад