Question

в треугольнике АBC медиана AD равна половине стороны BC . Докажите, что треугольник ABC прямоугольный

Answer 1

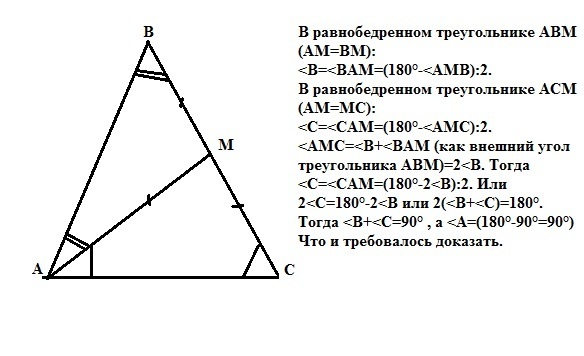
В равнобедренном треугольнике АВD  (АD=ВD):  
<В=<BAD=(180°-<АDВ):2.
В равнобедренном треугольнике АСD  (АD=DС):
<С=<СAD=(180°-<АDС):2.
<ADC=<B+<BAD (как внешний угол треугольника АВD)=2<B. Тогда
<С=<СAD=(180°-2<B):2. Или
2<C=180°-2<B или 2(<B+<C)=180°.
Тогда <B+<C=90° , а <A=(180°-90°=90°)
Что и требовалось доказать.