Вычислить приближенно(через дифференциал). Через калькулятор я и сам могу посчитать, нужно решение
Приложения:
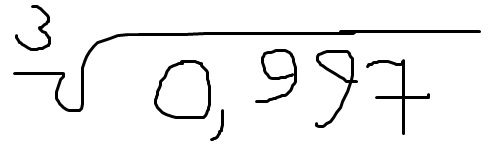
Ответы
Ответ дал:
0
Рассмотрим ![f(x)= sqrt[3]{x} f(x)= sqrt[3]{x}](https://tex.z-dn.net/?f=f%28x%29%3D+sqrt%5B3%5D%7Bx%7D+) .
.  - приближенное от числа 0,997,
- приближенное от числа 0,997, 
Значение функции в точке х0=1:![f(x_0)= sqrt[3]{1} =1 f(x_0)= sqrt[3]{1} =1](https://tex.z-dn.net/?f=f%28x_0%29%3D+sqrt%5B3%5D%7B1%7D+%3D1)
Вычислим производную функции![f'(x)=( sqrt[3]{x} )'= dfrac{1}{3^{2/3}} f'(x)=( sqrt[3]{x} )'= dfrac{1}{3^{2/3}}](https://tex.z-dn.net/?f=f%27%28x%29%3D%28+sqrt%5B3%5D%7Bx%7D+%29%27%3D+dfrac%7B1%7D%7B3%5E%7B2%2F3%7D%7D+)
Производная функции в точке х0=1:
Тогда приближенно это будет

Значение функции в точке х0=1:
Вычислим производную функции
Производная функции в точке х0=1:
Тогда приближенно это будет
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад