Точка K-cередина гипотенузы АВ прямоугольного труегольника АВС.Отрезок КМ перпендикулярен плоскости этого треугольника.Проведите через точку М перпендикуляры к прямым AC и BC и найдите их длины,если АС=8,BC=6,KM=5!!!
Ответы
Ответ дал:
0
Ответ:
МР = √41; МЕ = √34
Объяснение:
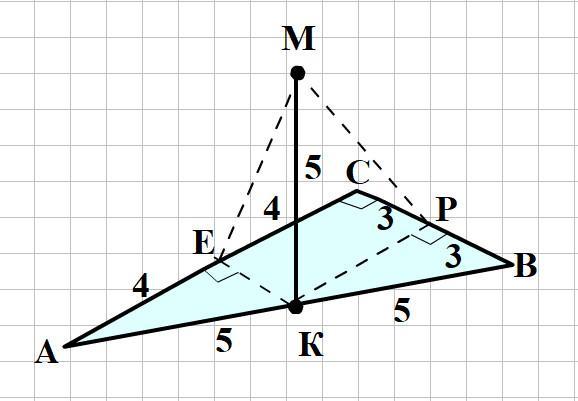
Смотри рисунок на прикреплённом фото.
Найдём гипотенузу АВ = √(АС² + ВС²) = √(8² + 6²) = 10
Из точки К проведём перпендикуляры КР и КЕ соответственно к сторонам ВС и АС. КР и КЕ являются средними линиями в ΔАВС.
КР = 0,5АС = 4; КЕ = 0,5ВС = 3.
Проведём наклонные МР и МЕ, которые и являются расстояниями от точки М до прямых ВС и АС, так как по теореме о 3-х перпендикулярах ВС ⊥ КР ⇒ ВС ⊥ МР и АС ⊥КЕ ⇒ АС ⊥МЕ.
Найдём МР и МЕ по теореме Пифагора.
МР = √(КР² + КМ²) = √(4² + 5²) = √41
МЕ = √(КЕ² + КМ²) = √(3² + 5²) = √34
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад