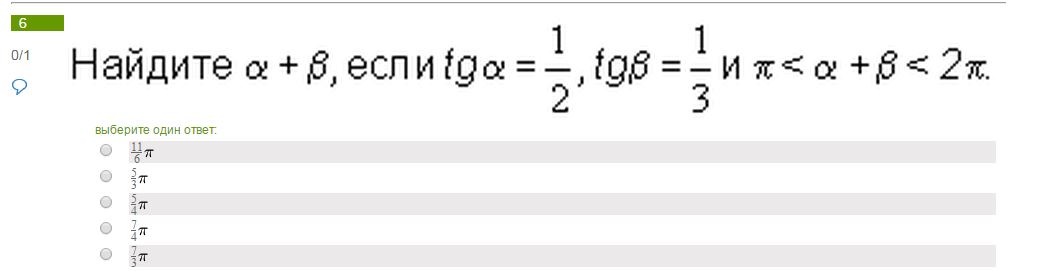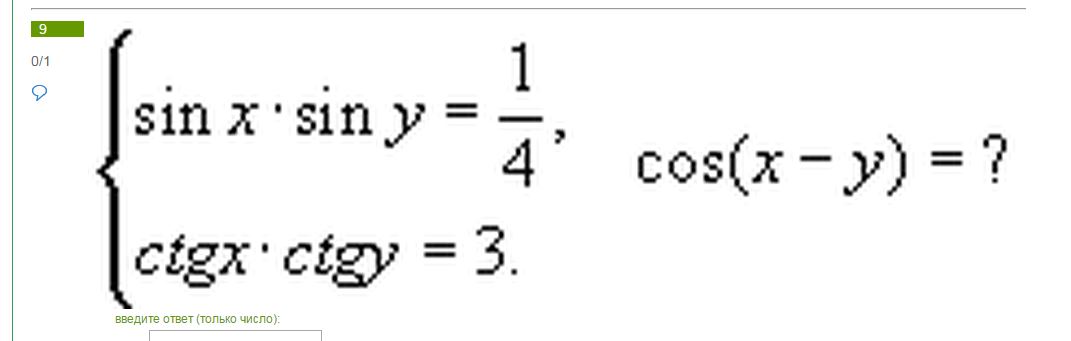Ответы
Ответ дал:
0
Ответ дал:
0
Громадное спасибо!
Ответ дал:
0
1)tg(a+b)=(tga+tgb)/(1-tgatgb)=(1/2+1/3):(1-1/2*1/3)=(3/6+2/6):(1-1/6)=5/6:5/6=1
a+b=π/4+πn U π<a+b<2π⇒a+b=5π/4
2)sinxsiny=1/4
ctgx*ctgy=cosxcosy/sinxsiny=3⇒cosxcosy=3*1/4=3/4
cos(x-y)=cosxcosy+sinxsiny=3/4+1/4=1
a+b=π/4+πn U π<a+b<2π⇒a+b=5π/4
2)sinxsiny=1/4
ctgx*ctgy=cosxcosy/sinxsiny=3⇒cosxcosy=3*1/4=3/4
cos(x-y)=cosxcosy+sinxsiny=3/4+1/4=1
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад