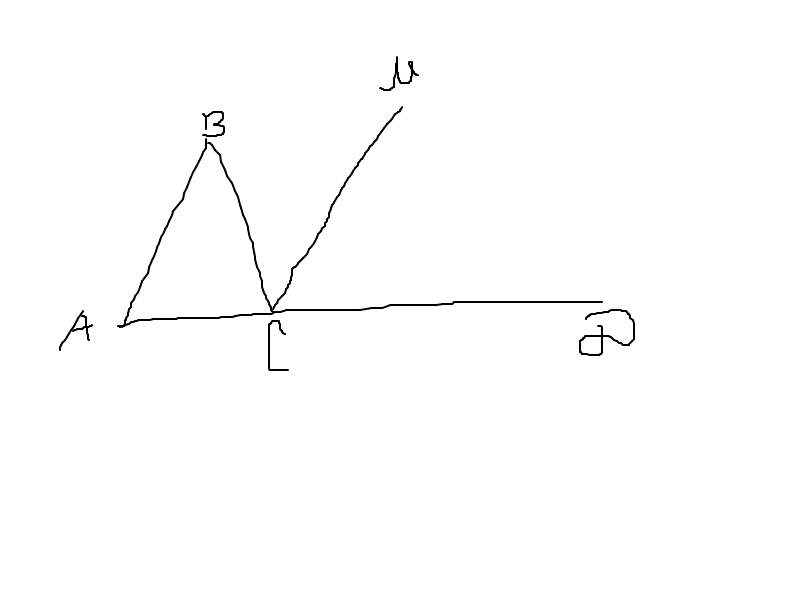
Дан треугольник ABC-равнобедренный. CM параллельна AB угол BCM 54 градуса угол MCD 36 градусов. Найдите угол A угол B и угол C.
Приложения:
Ответы
Ответ дал:
0
Примем за истинные утверждения из "дано":
1. Треугольник АВС - равнобедренный
2. СМ параллельна АВ.
3. Угол ВСМ равен 54 градуса.
Тогда <АВС=<ВСМ, как внутренние накрест лежащие при параллельных АВ и СМ и секущей ВС. Итак, угол В треугольника АВС = 54° В ЛЮБОМ СЛУЧАЕ.
Далее имеем варианты:
а) <С=<B=54°, тогда <A=72°. Ответ: <A=72°,<B=54°, <С=54°.
b) <A=<C= (180°-54°):2 = 63°. Ответ: <A=63°,<B=54°, <С=63°.
c) <A=<B=54°, тогда <C=72°. Ответ: <A=54°,<B=54°, <С=72°.
Если сторона СD угла МСD является продолжением стороны АС треугольника АВС,то утверждение: "угол MCD=36° ложно, так как тогда треугольник АВС прямоугольный (54°+36°=90°), угол В В ЛЮБОМ СЛУЧАЕ равен 54° и треугольник АВС НЕ МОЖЕТ БЫТЬ равнобедренным.
Если сторона СD угла МСD НЕ является продолжением стороны АС треугольника АВС,то данные об этом угле являются лишними для решения этой задачи.
1. Треугольник АВС - равнобедренный
2. СМ параллельна АВ.
3. Угол ВСМ равен 54 градуса.
Тогда <АВС=<ВСМ, как внутренние накрест лежащие при параллельных АВ и СМ и секущей ВС. Итак, угол В треугольника АВС = 54° В ЛЮБОМ СЛУЧАЕ.
Далее имеем варианты:
а) <С=<B=54°, тогда <A=72°. Ответ: <A=72°,<B=54°, <С=54°.
b) <A=<C= (180°-54°):2 = 63°. Ответ: <A=63°,<B=54°, <С=63°.
c) <A=<B=54°, тогда <C=72°. Ответ: <A=54°,<B=54°, <С=72°.
Если сторона СD угла МСD является продолжением стороны АС треугольника АВС,то утверждение: "угол MCD=36° ложно, так как тогда треугольник АВС прямоугольный (54°+36°=90°), угол В В ЛЮБОМ СЛУЧАЕ равен 54° и треугольник АВС НЕ МОЖЕТ БЫТЬ равнобедренным.
Если сторона СD угла МСD НЕ является продолжением стороны АС треугольника АВС,то данные об этом угле являются лишними для решения этой задачи.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад