Ответы
Ответ дал:
0
479 (1)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:

Ответ: 30 или 150 градусов
481
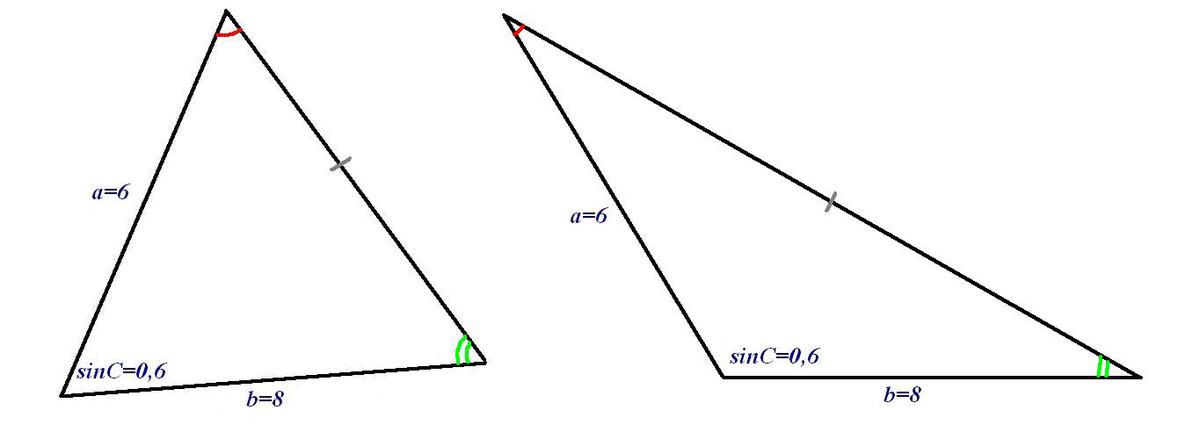
Если а=6, b=8, sinC=0,6, то:
Так как синус и острого и тупого угла положителен, то решение распадается на два случая: 1) с положительным косинусом и острым углом; 2) с отрицательным косинусом и тупым углом.
Чтобы найти третью сторону треугольника используем теорему косинусов, чтобы найти два других синуса - теорему синусов:


Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:
Ответ: 30 или 150 градусов
481
Если а=6, b=8, sinC=0,6, то:
Так как синус и острого и тупого угла положителен, то решение распадается на два случая: 1) с положительным косинусом и острым углом; 2) с отрицательным косинусом и тупым углом.
Чтобы найти третью сторону треугольника используем теорему косинусов, чтобы найти два других синуса - теорему синусов:
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад
