Решить тригонометрическое уравнение.
Я сама вроде как решила, проблема возникает с определением, какие екорни нужные, а какие не очень. Если не сложно, объясните это с помощью решения ур-ия по ОДЗ, а не с помощью подстановки полученных корней в ур-ие ОДЗ.
Приложения:
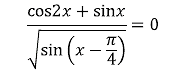
Ответы
Ответ дал:
0
ОДЗ
sin(x-π/4)>0
2πn<x-π/4<π+2πn
π/4+2πn<x<5π/4+2πn
cos2x+sinx=0
1-2sin²x+sinx=0
sinx=a
2a²-a-1=0
D=1+8=9
a1=(1-3)/4=-1/2⇒sinx=-1/2⇒x=(-1)^n+1*π/6+πn∉ОДЗ
a2=(1+3)/4=1⇒sinx=1⇒x=π/2+2πn
sin(x-π/4)>0
2πn<x-π/4<π+2πn
π/4+2πn<x<5π/4+2πn
cos2x+sinx=0
1-2sin²x+sinx=0
sinx=a
2a²-a-1=0
D=1+8=9
a1=(1-3)/4=-1/2⇒sinx=-1/2⇒x=(-1)^n+1*π/6+πn∉ОДЗ
a2=(1+3)/4=1⇒sinx=1⇒x=π/2+2πn
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад