Question

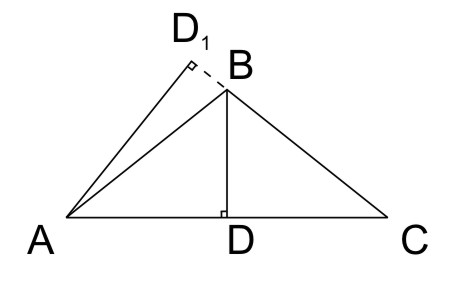
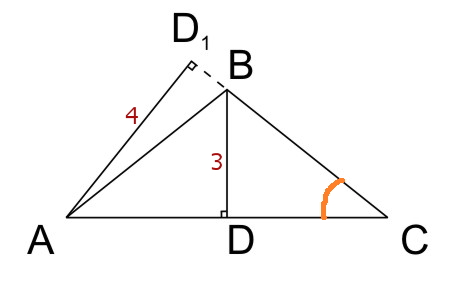
В равнобедренном треугольнике высота, опущенная на основание равна 3 м, а высота, опущенная на боковую сторону, равна 4 м. Найдите стороны этого треугольника.

Источник: Крамор В.С. Повторяем и систематизируем школьный курс геометрии, М., 1992, с. 59

... если не затруднительно, то распишите решение по-подробней, извиняюсь...

Answer 1

в равнобедренном треугольнике фишка в том, что получаются прямоугольные треугольники с общим (равным) острым углом, т.е. подобные)))
AD / BD = 4/3 = AC / BC
3*AC = 4*BC
и из равнобедренности данного треугольника следует, что AD=DC
AC = 2DC
BC² = BD² + DC²
(3*AC/4)² = 9 + (AC/2)²
9*AC²/16 = 9 + AC²/4
9*AC² = 9*16 + 4*AC²
AC² = 9*16/5
AC = 12/√5 = 12√5 / 5 = 2.4√5
BC² = 9 + (1.2√5)² = 9 + 1.44*5 = 9+7.2 = 16.2
BC = 0.1√1620 = 1.8√5 = AB

Answer 2

а с другой стороны -- это ведь не учебник, а "повторяем и систематизируем...", т.е. считается, что уже знаем больше, чем можно предположить))) хотя, момент есть))) посмотрю обязательно...

Answer 3

... там что-то "мала-мала" проблемы с выставлением задачи, я её выставил, да её удалили, в связи с тем, что с тем, что там была ссылка на данную задачу, а может и не только с этим... если не восстановят, возможно и не буду заново спрашивать, склоняюсь в точности к вашей последней мысли, что ключевое слов тут "повторение", то-есть что, именно — можно использовать кое-что и из "остаточных" хотя ещё и не "повторённых и систематизированных" школьных знаний...

Answer 4

ок) мне было интересно с Вами общаться...