Ответы
Ответ дал:
35
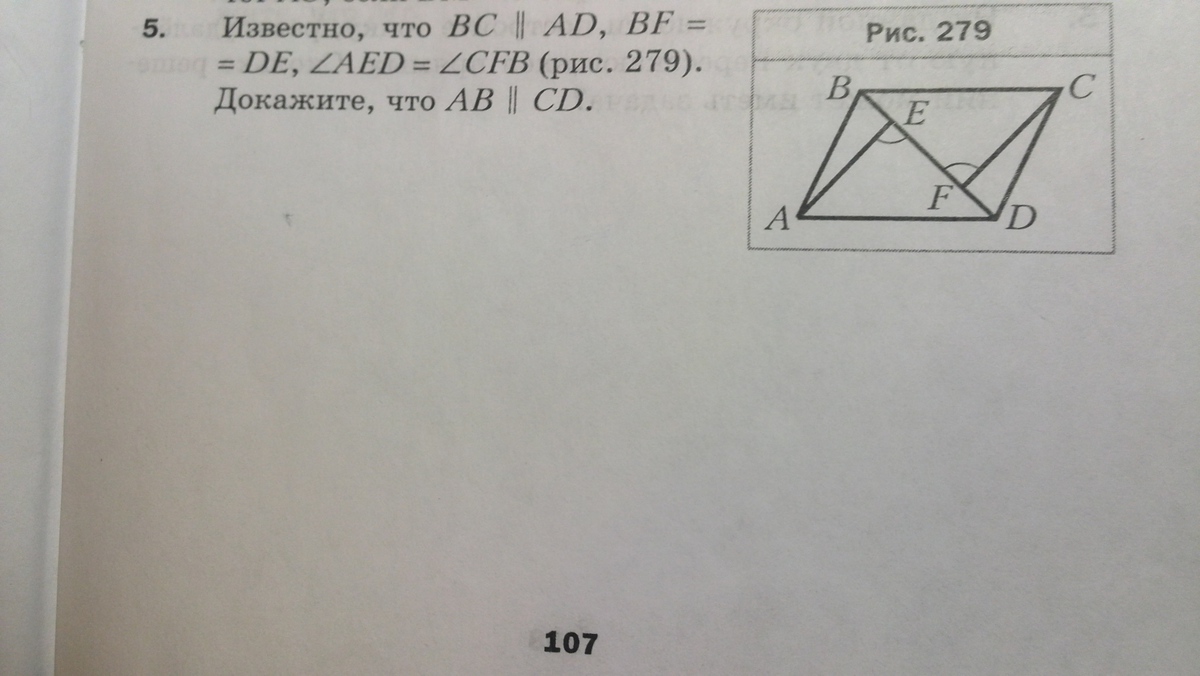
Рассмотрим два треугольника ΔАЕD и ΔВСD.
ВF = DE (по условию)
∠BFC = ∠AED (по условию)
∠FBC = ∠EDA как накрест лежащие между параллельными прямыми ВС и AD и секущей BD.
ΔАЕD = ΔВСD по стороне и двум прилежащим к ней углам.
Значит BC = AD.
В четырехугольнике ABCD противоположные стороны BC и AD равны и параллельны. Следовательно четырехугольник ABCD является параллелограммом.
Две другие противоположные стороны в параллелограмме ABCD также равны и параллельны.
Значит AB║CD, что и требовалось доказать.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад