Question

исследовать функцию и построить график y=x^4-2x^2-3

Answer 1

1. Обсласть опрежедения функции: множество всех действительных чисел.
2. четность функции
$y(-x)=(-x)^4-2(-x)^2-3=x^4-2x^2-3=y(x)$
Итак, функция четная.
3. Точки пересечения с осью Ох и Оу.
3.1. С осью Ох (у=0)
$x^4-2x^2-3=0$
Через дискриминант
$D=b^2-4ac=4+12=16 \\ x=\pm \sqrt{3}$

$(-\sqrt{3};0),\,\,(\sqrt{3};0)$ точки с соью Ох

3.2. Точки пересения с осью Оу (х=0)
$y=-3$
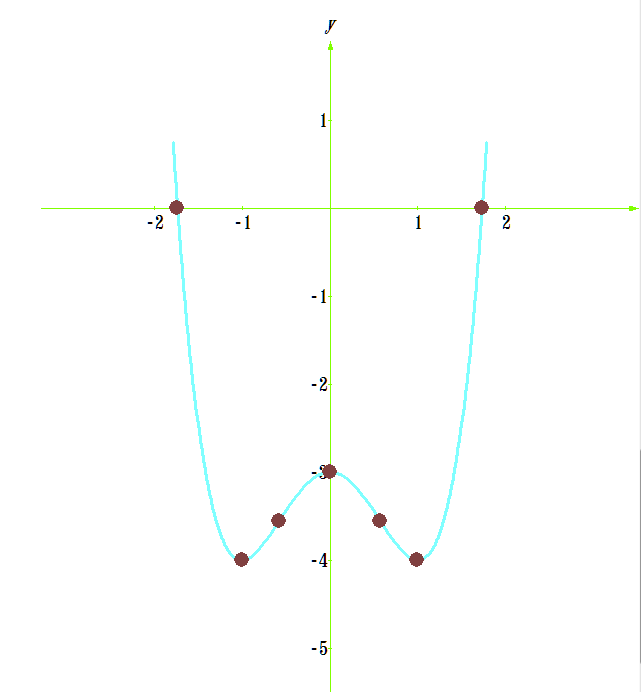
(0;-3) - точки пересечения с осью Оу

4. Критические точки(возрастание и убывание функции)
$y'=4x^3-4x$
Приравняем к нулю
$4x(x^2-1)=0 \\ x_1=0 \\ x_2=1 \\ x_3=-1$

_-_(-1)__+__(0)__-_(1)__+__>

Итак, функция возрастает на промежутке $x \in (-1;0)\cup (1;+\infty)$, убывает $x \in (-\infty;-1)\cup(0;1)$. В точке х=-1 и х=1 функция имеет локальный минимум, а в точке х=0 - локальный максимум
5. Точки перегиба
$y''=12x^2-4 \\ y''=0 \\ 4(3x-1)=0 \\ x=\pm \frac{ \sqrt{3} }{3}$

Вертикальных, горизональных и наклонных асимптот нет.