Найти точки максимума и минимума функции f(x) на отрезке [a;b] и наибольшее и наименьшее значение функции на этом отрезке.
Приложения:
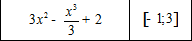


yanaaleksandrov:
первое .ОДЗ х принадлежит R производная = 6x-x^2 приравняем к 0 6x-x^2=0 x(6-x)=0 x=0 или x=6 точка х=6 не входит в промежуток, ее исключаем. берем значения произ. до 0 - получается сщ знаком (-),после 0- со знаком (+), значит точка 0- точка минимума
точка х=6 - это точка максимума ф-ции, но она не входит в наш промежуток теперь найдем значение ф-ции от -1;3; и 0 f(-1)=3-1/3+2=4 2/3 f(3)=3*9-9+2=11 f(0)=2 значит наиб значение-f(3)=11, наим. значение f(0)=2
по второму заданию расписывать не буду. ОДЗ х принадл R произв = 1/2*х^2-x 1/2*x^2-x=0 x(1/2x-1)=0 x=0 или x=2 точка 2 не входит в отрезок. смотрим знаки произвлдной в промежутках до точки 0- знак (+), от 0 до 2 знак минус, после точки 2 знак плюс. значит ф-ция возрастает на прмеж от - бескон. до 0 и от 2 до + бесконеч. точка 0-точка максимума, точка 2 точка минимума.
найдем значение функции в точках -2;0;1 f(-2)= -4/3-2+2= -4/3= - 1 1/3 f(0)=2 f(1)=1/6-1/2+2=1 2/3 наиб знач f(0)=2 наим. значение f(-2)= - 1 1/3
в последнем ОДЗ:х принадлежит R. произв= 3x^2+6x-45 3x^2+6x-45=0 x1=(-6+24)/6=3 x2=(-6-24)/6=5 оба значения не входят в промежуток мы можем найти мин и макс ф-ции в целом
смотрим знаки приозв в промежутках до -5 знак минус от -5 до 3 знак минус , после 3 знак плюс, значит ф-ция убывает от минус бескон. до 3 и возраст от 3 до плюс бескон. точка 3-точка минимума ф-ции. в промежуток не попали точки экстремума ф-ции, поэтому найдем значение ф-ции на концах отрезка. f(-2)=87 f(2)= -77 значит наим знач f(2)=-77 наиб f(-2)=87
Ответы
Ответ дал:
1
1) Находим производную функцию

2) Производная равна нулю

6 - не входит в промежуток
Найдем значение функции в точке х=-1, х=0 и х=3
y(0)=2
y(-1)=16/3
y(3)=20
Итак, наименьшее значение функции 2, а наибольшее 20
Производная функции

Производная равна нулю

x=2 - не входит в промежуток
найдем значение функции в точке х=0, х=-2 и х=1
y(0)=2
y(-2)=-4/3
y(1)=5/3
Итак, наибольшее значение функции х=2, а наименьшее -4/3
1) Производная функции

Приравниваем к нулю

По т. Виета
x1=-5 - не входит в промежуток
x2=3 - не входит в промежуток
Найдем значение функции в точке х=-2 и х=2
y(-2)=87 - наибольшее
y(2)=-77 - наименьшее
2) Производная равна нулю
6 - не входит в промежуток
Найдем значение функции в точке х=-1, х=0 и х=3
y(0)=2
y(-1)=16/3
y(3)=20
Итак, наименьшее значение функции 2, а наибольшее 20
Производная функции
Производная равна нулю
x=2 - не входит в промежуток
найдем значение функции в точке х=0, х=-2 и х=1
y(0)=2
y(-2)=-4/3
y(1)=5/3
Итак, наибольшее значение функции х=2, а наименьшее -4/3
1) Производная функции
Приравниваем к нулю
По т. Виета
x1=-5 - не входит в промежуток
x2=3 - не входит в промежуток
Найдем значение функции в точке х=-2 и х=2
y(-2)=87 - наибольшее
y(2)=-77 - наименьшее
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад