Question

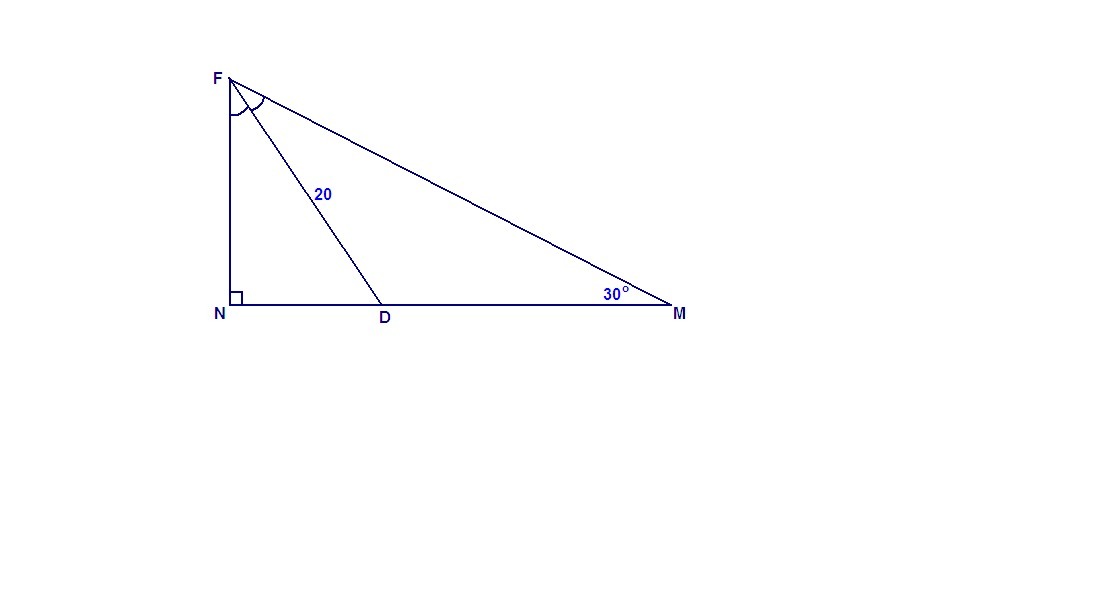
В прямоугольном треугольнике MNF,угол N=90 угол M=30.FD-биссектриса треугольника,FD=20 см.Найдите длину катета MN.

Answer 1

Сумма острых углов прямоугольного треугольника равна 90°, тогда

∠NFM = 90° - ∠M = 90° - 30° = 60°

FD - биссектриса, поэтому

∠NFD = ∠MFD = 60°/2 = 30°

В ΔFDM два угла равны (∠DFM = ∠DMF = 30°), значит треугольник равнобедренный:

DM = FD = 20 см

В прямоугольном треугольнике NFD по свойству катета, лежащего напротив угла в 30°

ND = 1/2 FD = 1/2 · 20 = 10 см

MN = ND + DM = 10 + 20 = 30 см