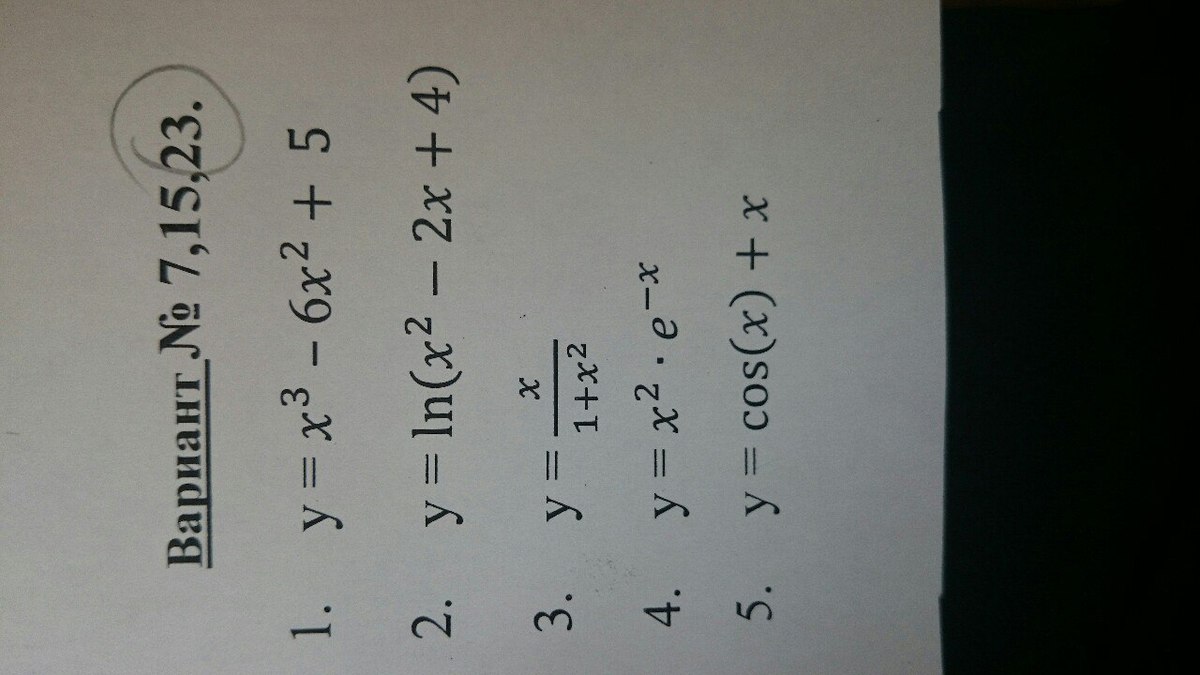Ответы
Ответ дал:
1
1) y '=(x³ - 6x²+5)' = (x³)' - (6x²)' +(5)' = 3x² - 6*2x +0 =3x(x - 2)
2) y '=(ln(x² -2x +4))'= 1/(x² -2x +4)*(x² -2x +4)' = 2(x -1)/(x² -2x +4)
3) y ' =( (x)'*(1+x²)-x*(1+x²)' )/ (1+x²)² = (1-x²)/(1+x²)²
4) y ' = (x²)'*(e)^(-x) +x²*((e)^(-x))'= 2x*(e)^(-x) - x²*(e)^(-x) =x*(e)^(-x)*(2-(e)^(-x))
5) y' =(cos(x) +x)' = (cos(x))' +(x)' = -cos(x) +1
2) y '=(ln(x² -2x +4))'= 1/(x² -2x +4)*(x² -2x +4)' = 2(x -1)/(x² -2x +4)
3) y ' =( (x)'*(1+x²)-x*(1+x²)' )/ (1+x²)² = (1-x²)/(1+x²)²
4) y ' = (x²)'*(e)^(-x) +x²*((e)^(-x))'= 2x*(e)^(-x) - x²*(e)^(-x) =x*(e)^(-x)*(2-(e)^(-x))
5) y' =(cos(x) +x)' = (cos(x))' +(x)' = -cos(x) +1
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад