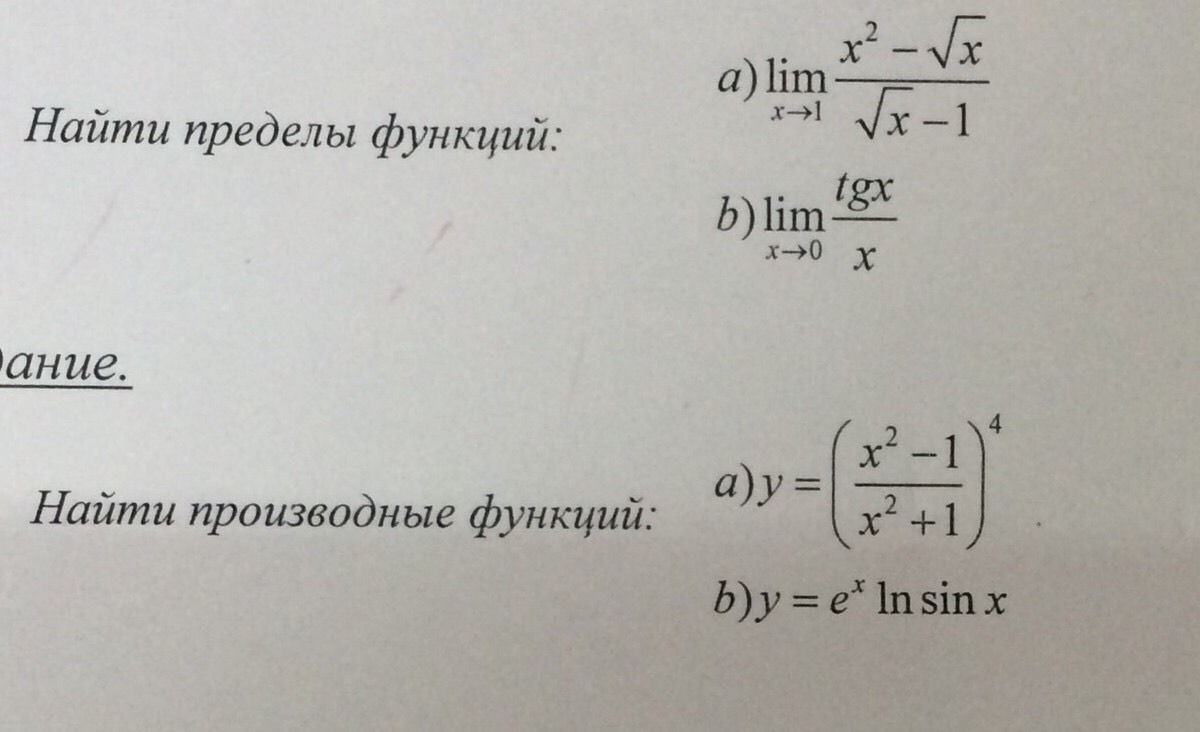Ответы
Ответ дал:
1
а)
![lim_{x\to1}\frac{x^2-\sqrt{x}}{\sqrt{x}-1}=[\frac{0}{0}]=lim_{x\to1}\frac{(x^2-\sqrt{x})'}{(\sqrt{x}-1)'}=lim_{x\to1}\frac{2x-\frac{1}{2\sqrt{x}}}{\frac{1}{2\sqrt{x}}}=\frac{2*1-\frac{1}{2*1}}{\frac{1}{2*1}}=3 lim_{x\to1}\frac{x^2-\sqrt{x}}{\sqrt{x}-1}=[\frac{0}{0}]=lim_{x\to1}\frac{(x^2-\sqrt{x})'}{(\sqrt{x}-1)'}=lim_{x\to1}\frac{2x-\frac{1}{2\sqrt{x}}}{\frac{1}{2\sqrt{x}}}=\frac{2*1-\frac{1}{2*1}}{\frac{1}{2*1}}=3](https://tex.z-dn.net/?f=lim_%7Bx%5Cto1%7D%5Cfrac%7Bx%5E2-%5Csqrt%7Bx%7D%7D%7B%5Csqrt%7Bx%7D-1%7D%3D%5B%5Cfrac%7B0%7D%7B0%7D%5D%3Dlim_%7Bx%5Cto1%7D%5Cfrac%7B%28x%5E2-%5Csqrt%7Bx%7D%29%27%7D%7B%28%5Csqrt%7Bx%7D-1%29%27%7D%3Dlim_%7Bx%5Cto1%7D%5Cfrac%7B2x-%5Cfrac%7B1%7D%7B2%5Csqrt%7Bx%7D%7D%7D%7B%5Cfrac%7B1%7D%7B2%5Csqrt%7Bx%7D%7D%7D%3D%5Cfrac%7B2%2A1-%5Cfrac%7B1%7D%7B2%2A1%7D%7D%7B%5Cfrac%7B1%7D%7B2%2A1%7D%7D%3D3)
б)
2.
a)

б)

б)
2.
a)
б)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад