Исследовать расширенные матрицы систем линейных уравнений и в случае совместности уравнений решить их.
Приложения:
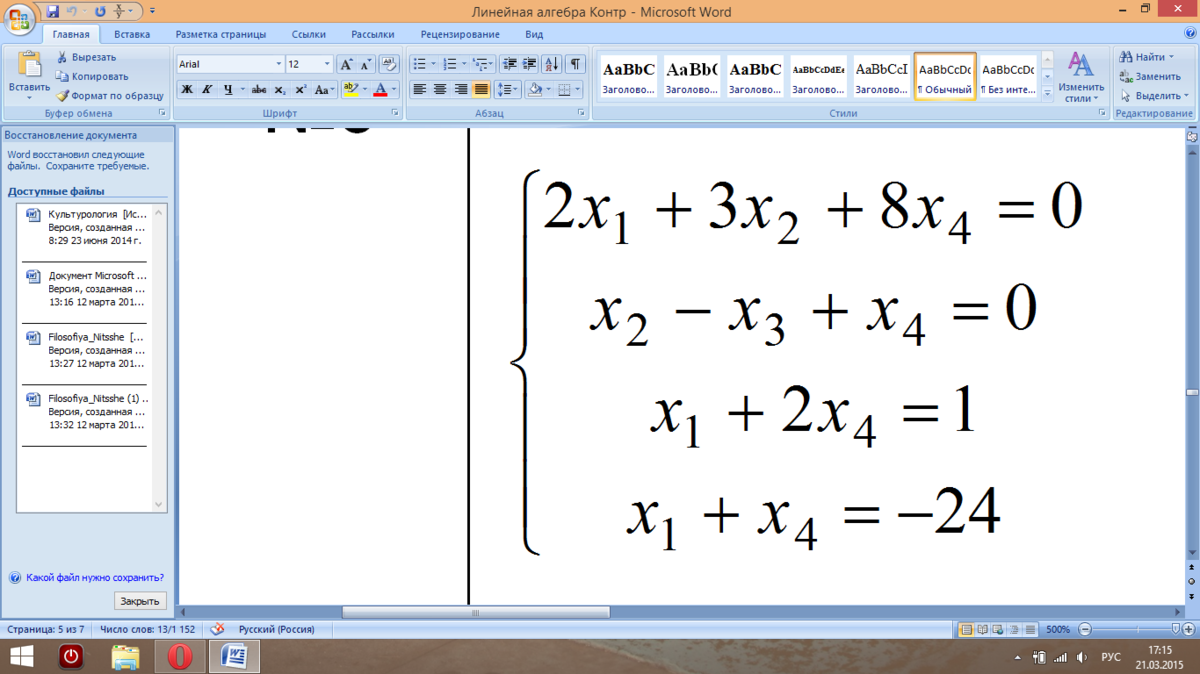
Ответы
Ответ дал:
0
Ранг расширенной матрицы равен рангу основной матрицы и равны количеству неизвестных, система совместна и имеет единственное решение
gal94:
а как решать я так и не поняла.а поподробней?
Матричный метод, выписываем все коэффициенты при неизвестных + свободные коэффициенты (для расширенной матрицы), приводим матрицу к треугольному виду (под диагональю нули). Ранг это "количество ненулевых строк" Записываем новую систему с коэффициентами треугольной матрицы и решаем ее, начиная снизу.
Вас заинтересует
2 года назад
7 лет назад
9 лет назад