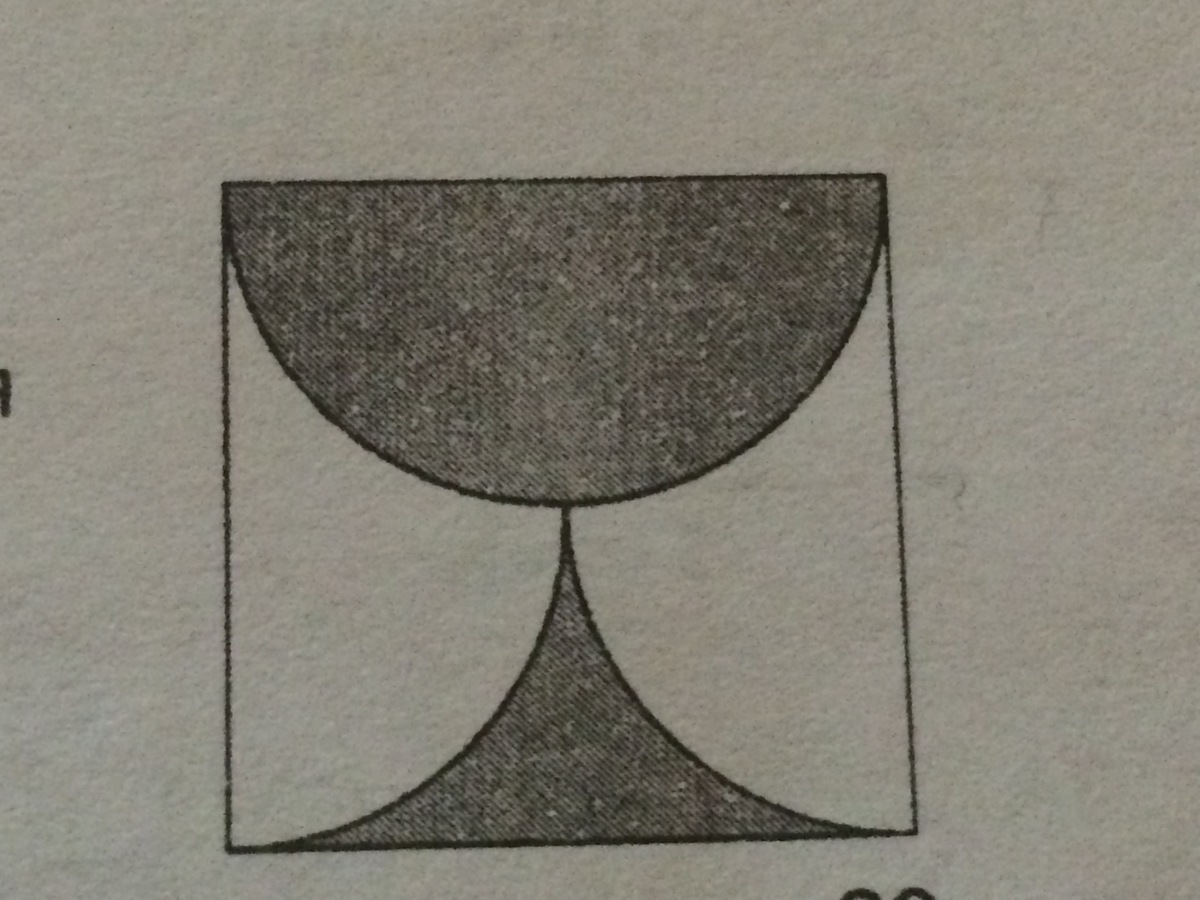
Закрашенная часть квадрата со стороной а(альфа) ограничена полуокружностью и двумя четвертями окружности. Чему равна площадь этой части?
Приложения:
Ответы
Ответ дал:
1
Площадь квадрата 
Полуокружность (верхняя часть заштрихованной области) имеет диаметр . Её площадь
. Её площадь 
Рассмотрим другой квадрат (см. рис.). Его сторона так же равна , а нижняя заштрихованная часть идентична нижней части заданного квадрата. Заштрихованная область ограничена двумя полуокружностями. Площадь этих полуокружностей равна
, а нижняя заштрихованная часть идентична нижней части заданного квадрата. Заштрихованная область ограничена двумя полуокружностями. Площадь этих полуокружностей равна  . Тогда площадь всей заштрихованной области - это разница площадей квадрата и двух полуокружностей.
. Тогда площадь всей заштрихованной области - это разница площадей квадрата и двух полуокружностей.

Отсюда площадь нижней заштрихованной части равна

Площадь всей заштрихованной области заданного квадрата равна

Полуокружность (верхняя часть заштрихованной области) имеет диаметр
Рассмотрим другой квадрат (см. рис.). Его сторона так же равна
Отсюда площадь нижней заштрихованной части равна
Площадь всей заштрихованной области заданного квадрата равна
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад