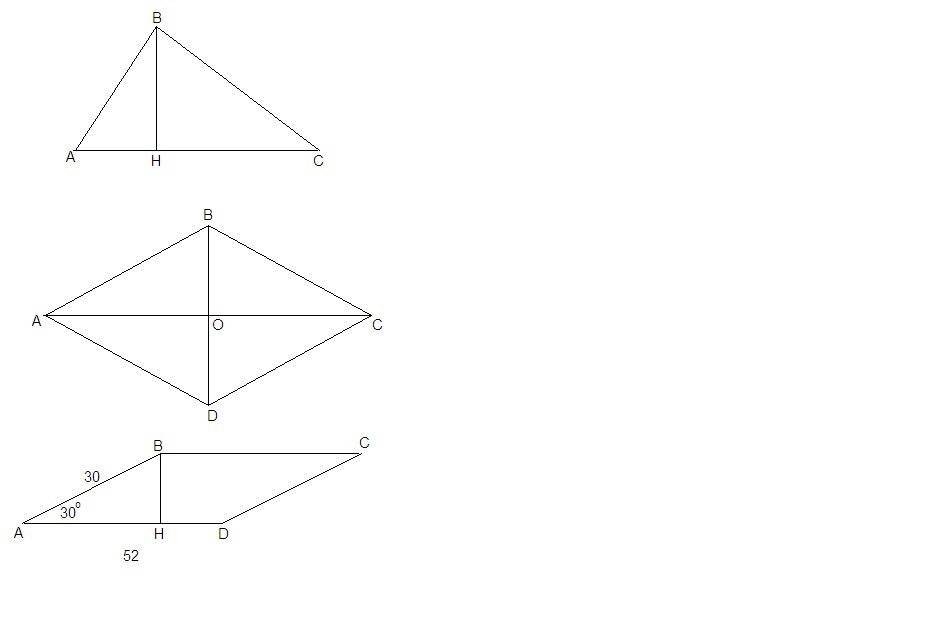
1) В треугольнике АВС сторона АС=7см, а высота равна 11 см. Вычислите площадь треугольника
2) Найдите площадь и периметр ромба, если его диагонали равна 8 и 10 см.
3) Смежные сторона параллелограмма 52 см и 30 см, а острый угол равен 30 градусов. Найдите площадь параллелограмма.

dobryajalizka: Это 3 задачи разные?

dobryajalizka: И еще в первой задаче высота опущена на сторону ас? Это важно

aleonamatveeva: Да это три разные

dobryajalizka: Так что там с высотой?

aleonamatveeva: Нет не опущина

dobryajalizka: Просто площадь по формуле половина основания на высоту

aleonamatveeva: Получается да

Ответы

Ответ дал: KuOV

1. Sabc = AC · BH / 2 = 7 · 11 / 2 = 38,5 см²

2. Sabcd = AC · BD /2 = 10·8/2 = 40 см²
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Поэтому
АО = АС/2 = 10/2 = 5 см
BO = BD/2 = 8/2 = 4 см
ΔABO: ∠AOB = 90°, по теореме Пифагора
AB = √(AO² + BO²) = √(25 + 16) = √41 см
Pabcd = 4·AB = 4√41 см

3. Проведем ВН⊥AD.
ΔАВН: ∠АНВ = 90°, ∠ВАН = 30°, ⇒ ВН = АВ/2 = 30/2 = 15 см (по свойству катета, лежащего напротив угла в 30°)
Sabcd = AD·BH = 52·15 = 780 см²

Приложения: