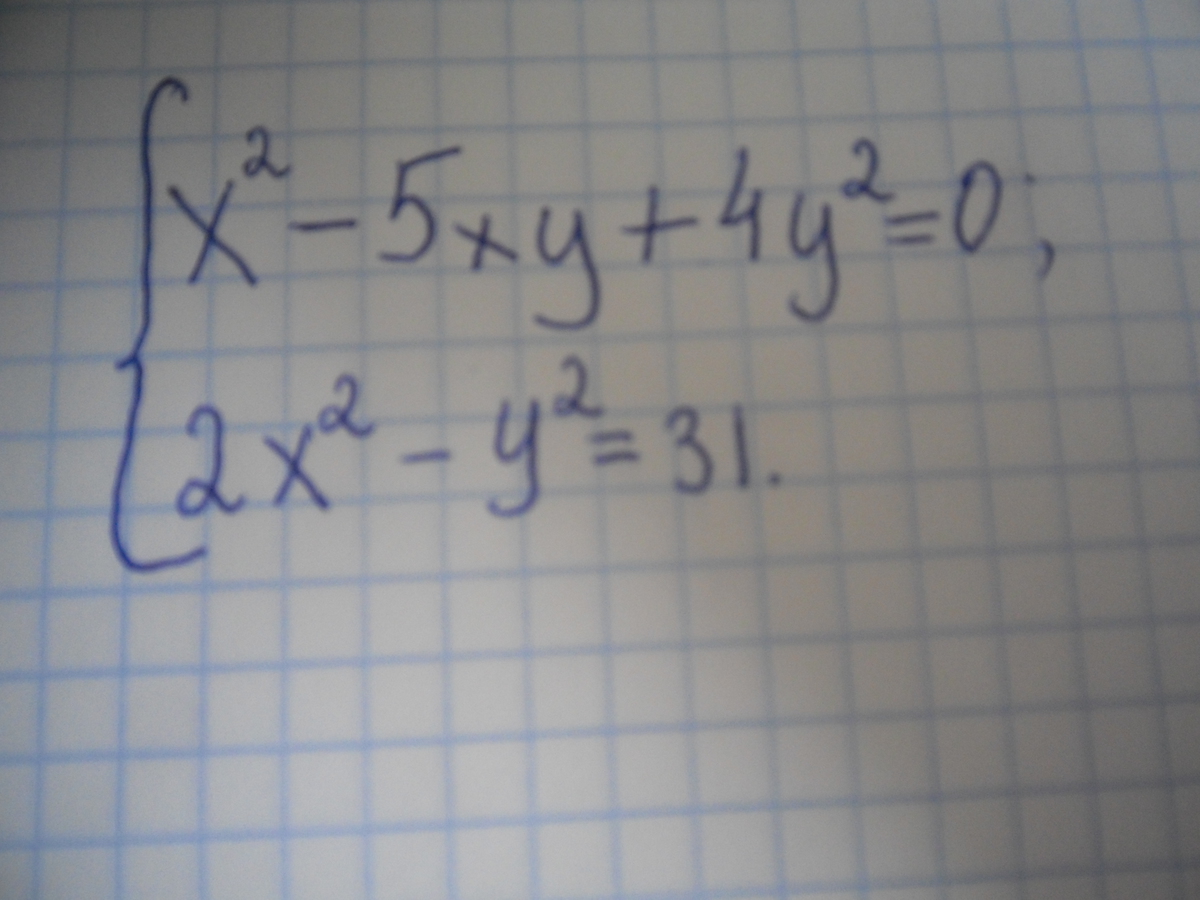Ответы
Ответ дал:
1
Решение системы в файле.
Приложения:
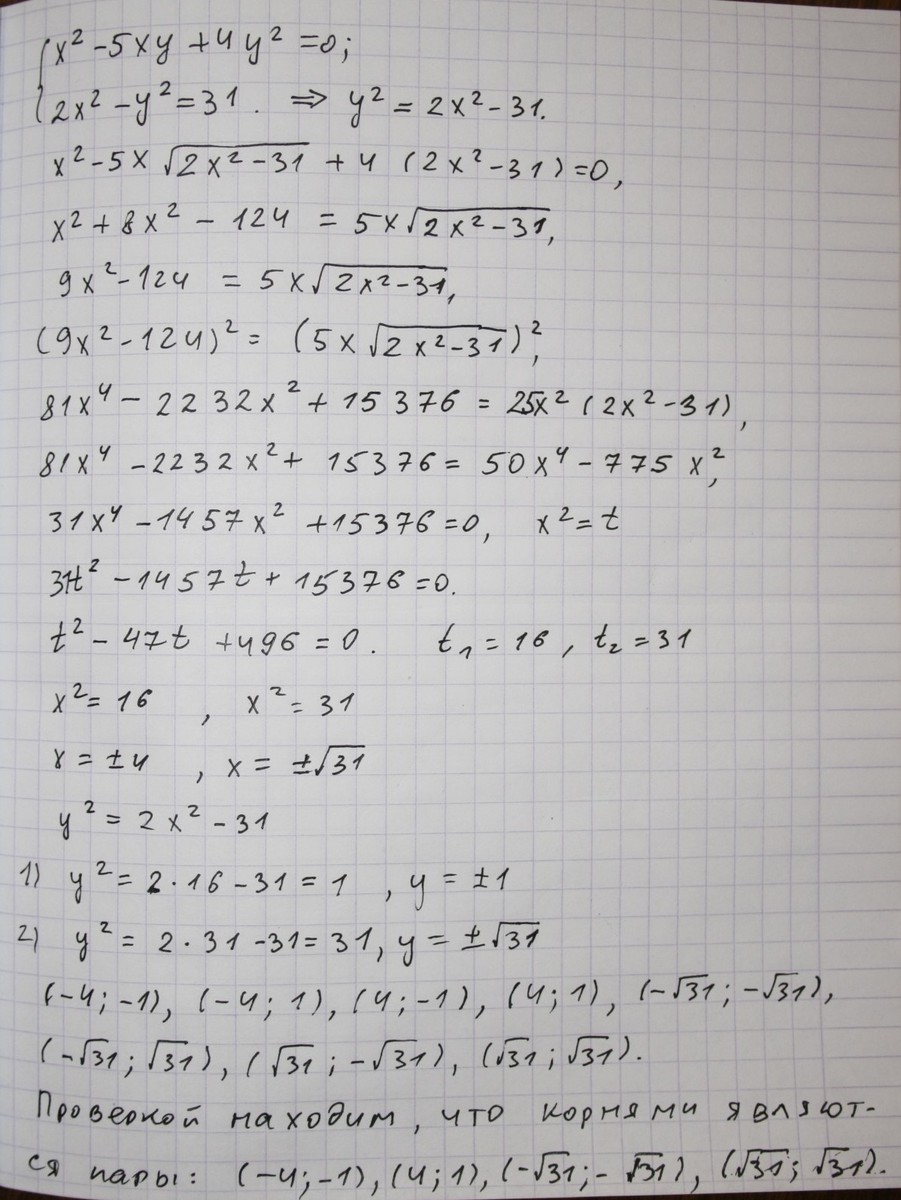
infern:
Во второй строчке после системы,там х^2+(что это за цифра?)
видимо вы имеете ввиду 8
так и подумала,решила уточнить,спасибо
Ответ дал:
1
{x²-5xy+4y²=0
{2x²-y²=31
1) Разделим обе части первого уравнения на у², предполагая, что у≠0.
Получим:
х² -5ху+4у²=0
у² у² у² у²
х² - 5х +4=0
у² у
Обозначим t=x , получим уравнение:
y
t²-5t+4=0
D=25-16=9
t₁=5-3=1 или х =1 х=у
2 у
t₂=5+3=4 или х =4 х=4у
2 у
2) Исходная система сводится к решению совокупности двух систем:
1) {x=y 2) {x=4y
{2x²-y²=31 {2x²-y²=31
2y²-y²=31 2(4y)²-y²=31
y²=31 31y²=31
y₁=√31 x₁=√31 y²=1
y₂=-√31 x₂=-√31 y₁=1 х₁=1
у₂=-1 х₂=-1
Ответ: х=√31 у=√31
х=-√31 у=-√31
х=1 у=1
х=-1 у=-1
{2x²-y²=31
1) Разделим обе части первого уравнения на у², предполагая, что у≠0.
Получим:
х² -5ху+4у²=0
у² у² у² у²
х² - 5х +4=0
у² у
Обозначим t=x , получим уравнение:
y
t²-5t+4=0
D=25-16=9
t₁=5-3=1 или х =1 х=у
2 у
t₂=5+3=4 или х =4 х=4у
2 у
2) Исходная система сводится к решению совокупности двух систем:
1) {x=y 2) {x=4y
{2x²-y²=31 {2x²-y²=31
2y²-y²=31 2(4y)²-y²=31
y²=31 31y²=31
y₁=√31 x₁=√31 y²=1
y₂=-√31 x₂=-√31 y₁=1 х₁=1
у₂=-1 х₂=-1
Ответ: х=√31 у=√31
х=-√31 у=-√31
х=1 у=1
х=-1 у=-1
сделайте проверку и убедитесь, что пары (1;1) и (-1;-1) не являются корнями системы.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад