Question

Вокруг шара описан цилиндр.Найдите отношение площади поверхности цилиндра к площади поверхности шара.
Пожаалуйста, помогите:))

Answer 1

Ответ:

3/2

Объяснение:

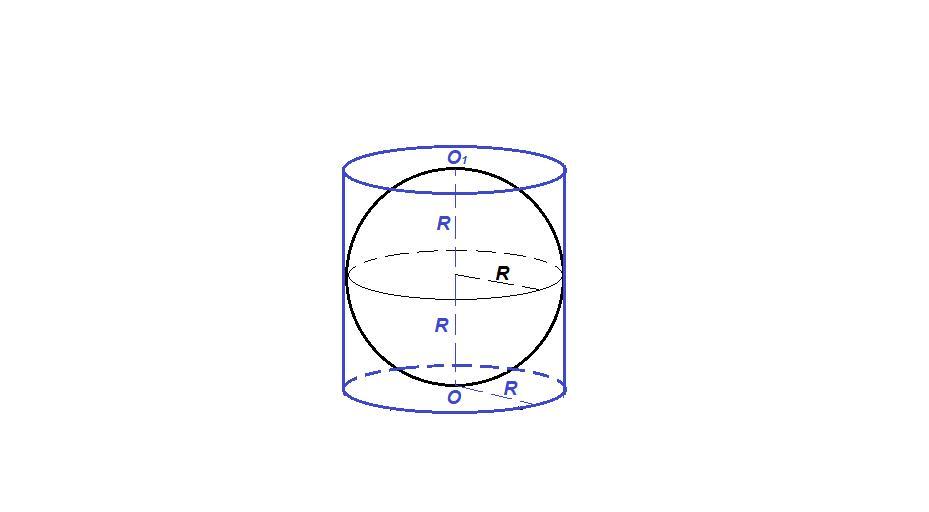
Если цилиндр описан вокруг шара, то радиус основания цилиндра равен радиусу шара, а высота цилиндра равна диаметру шара.

Пусть R - радиус шара, тогда радиус основания цилиндра тоже R, а высота цилиндра ОО₁ = 2R.

Площадь поверхности шара:

S₁ = 4πR²

Площадь поверхности цилиндра:

S₂ = Sбок. + 2Sосн.

S₂ = 2πR·OO₁ + 2·πR² = 2πR · 2R + 2πR² = 4πR² + 2πR² = 6πR²

$\dfrac{S_{2}}{S_{1}}=\dfrac{6\pi R^{2}}{4\pi R^{2}}=\dfrac{6}{4}=\dfrac{3}{2}$