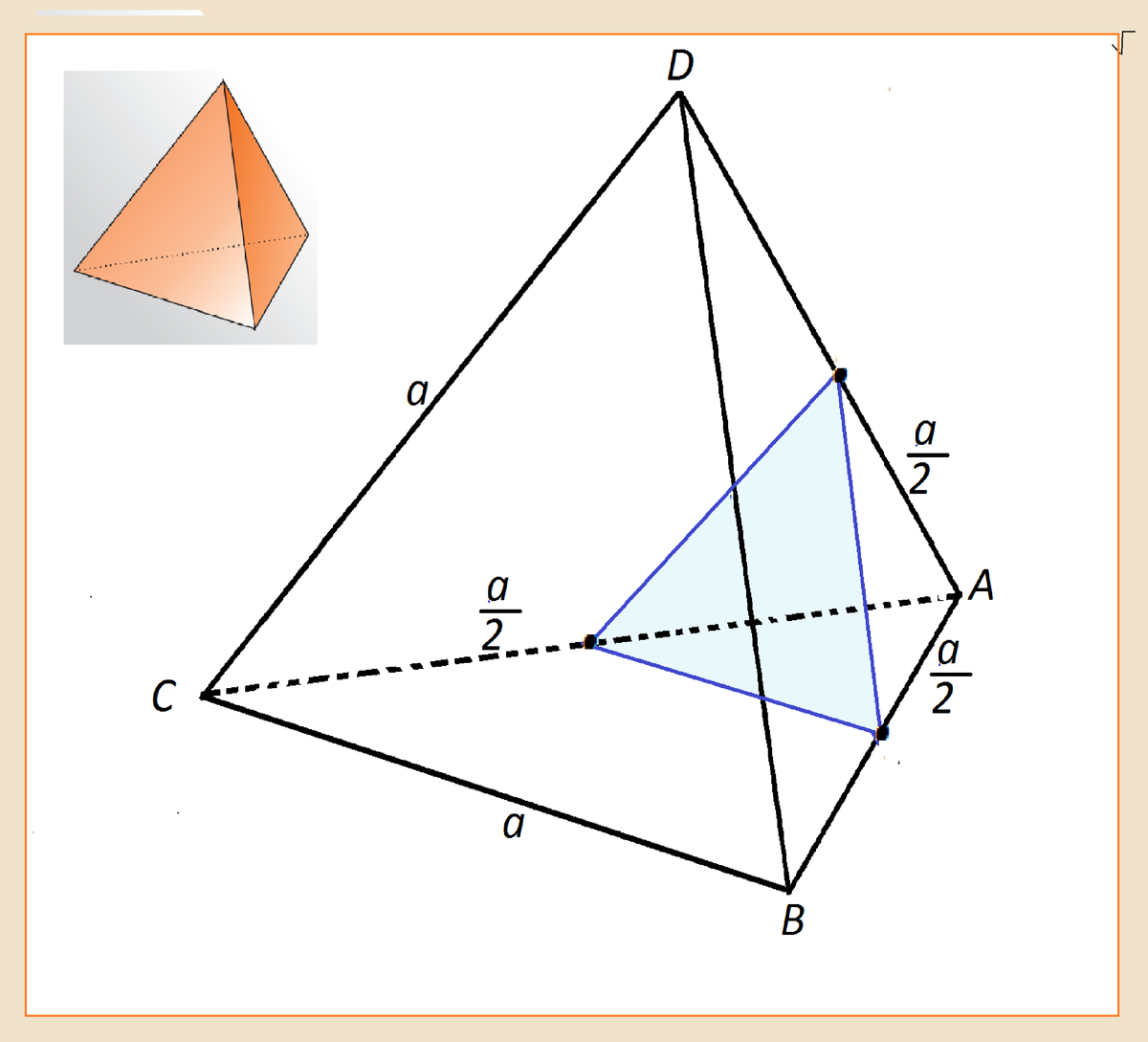
Ребро правильного тетраэдра DАВС равно а. Постройте сечение тетраэдра, проходящее через середины ребер DА и АВ параллельно ребру ВС, и найдите S этого сечения
Ответы
Ответ дал:
2
Тетраэдр называется правильным, если все его грани — равносторонние треугольники.
Каждая сторона построенного сечения - средняя линия треугольника. ограничивающего грань тетраэдра, и потому равна а/2.
Т.е. проведенное через середины ребер сечение - правильный треугольник со сторонами, равными а/2
Его площадь по формуле S=(a²√3):4 площади равностороннего треугольника:
S=(a/2)²√3):16
Каждая сторона построенного сечения - средняя линия треугольника. ограничивающего грань тетраэдра, и потому равна а/2.
Т.е. проведенное через середины ребер сечение - правильный треугольник со сторонами, равными а/2
Его площадь по формуле S=(a²√3):4 площади равностороннего треугольника:
S=(a/2)²√3):16
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад