В прямоугольном треугольнике высота и медиана,проведенные из прямого угла делят этот угол на три равные части.Площадь треугольника,образуемого вершиной
прямого угла и точками пересечения высоты и медианы с гипотенузой, равна 2 \sqrt{3}.Найдите площадь круга вписанного в исходный треугольник.
Ответы
Ответ дал:
7
ВАС=90
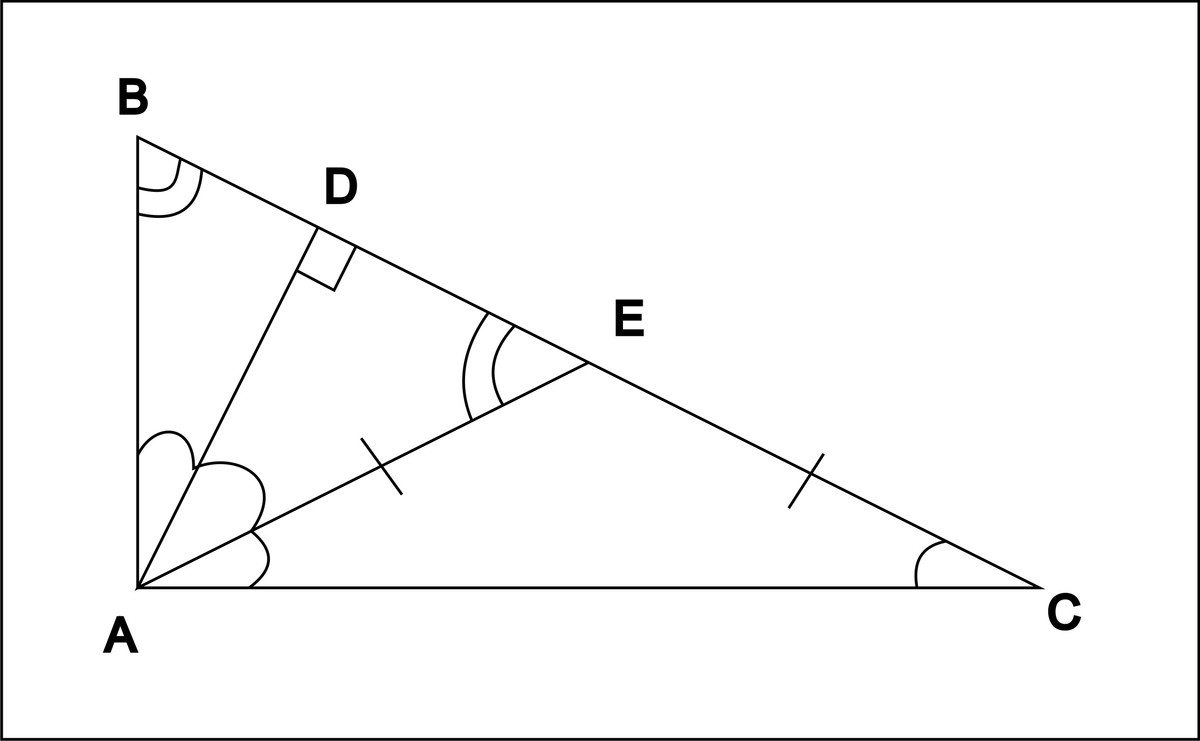
Т.к. угол ВАС делится на 3 равные части, то угол ВДА= углу ДАЕ= углу ЕАС=30.
Треугольник ВДА подобен ВАС по двум углам: ДВА=АВС, угол ВДА=ВАС=90 ,
=> угол ВСА= ДАВ=30
=>треугольник АЕС= равнобедренный , АЕ=АС
Треугольник ВДА= ЕДА по двум углам и стороне, ДА- общая, угол ВДА=ЕДА, угол ВАД=ЕАД.
=>ВД=ДЕ
обозначим ДЕ за х, тогда ВД=х, ЕС=2х, ЕА=2х
S треугольника ЕДА =(1/2)*ЕД*ДА=(1/2)*х*2х*cos30
(х^2)*(sqrt{3}/2)=2/sqrt{3}
х=2/sqrt{3}
(1/2)АС=АЕ*cos30=(4/sqrt{3})*(sqrt{3}/2)=2
=> AC=4
ВА=ВС*cos60=4x*(1/2)=(8/sqrt{3})*(1/2)=4/sqrt{3}
S треугольника АВС =(1/2)*АВ*АС=8/sqrt{3}
р (полупериметр)=(6+2sqrt{3})/sqrt{3}
r=S/p
r=8/(6+2sqrt{3})=4/(3+sqrt{3})
S круга=п*r^2=(16п)/((3+sqrt{3})^2)
Т.к. угол ВАС делится на 3 равные части, то угол ВДА= углу ДАЕ= углу ЕАС=30.
Треугольник ВДА подобен ВАС по двум углам: ДВА=АВС, угол ВДА=ВАС=90 ,
=> угол ВСА= ДАВ=30
=>треугольник АЕС= равнобедренный , АЕ=АС
Треугольник ВДА= ЕДА по двум углам и стороне, ДА- общая, угол ВДА=ЕДА, угол ВАД=ЕАД.
=>ВД=ДЕ
обозначим ДЕ за х, тогда ВД=х, ЕС=2х, ЕА=2х
S треугольника ЕДА =(1/2)*ЕД*ДА=(1/2)*х*2х*cos30
(х^2)*(sqrt{3}/2)=2/sqrt{3}
х=2/sqrt{3}
(1/2)АС=АЕ*cos30=(4/sqrt{3})*(sqrt{3}/2)=2
=> AC=4
ВА=ВС*cos60=4x*(1/2)=(8/sqrt{3})*(1/2)=4/sqrt{3}
S треугольника АВС =(1/2)*АВ*АС=8/sqrt{3}
р (полупериметр)=(6+2sqrt{3})/sqrt{3}
r=S/p
r=8/(6+2sqrt{3})=4/(3+sqrt{3})
S круга=п*r^2=(16п)/((3+sqrt{3})^2)
Приложения:
StalkerVrk:
Прости,вообще косяк, 2*на корень из 3.
ну давай я перерешаю сейчас
(8п)/(2+sqrt{3})
Есть такой ответ?
Есть такой ответ?
Почти, там 8п*(2-корень из 3)
это тоже самое, просто преобразовали, домножили на числитель и знаменатель на (2-корень из 3)
ВАС=90
Т.к. угол ВАС делится на 3 равные части, то угол ВДА= углу ДАЕ= углу ЕАС=30.
Треугольник ВДА подобен ВАС по двум углам: ДВА=АВС, угол ВДА=ВАС=90 ,
=> угол ВСА= ДАВ=30
=>треугольник АЕС= равнобедренный , АЕ=АС
Треугольник ВДА= ЕДА по двум углам и стороне, ДА- общая, угол ВДА=ЕДА, угол ВАД=ЕАД.
=>ВД=ДЕ
обозначим ДЕ за х, тогда ВД=х, ЕС=2х, ЕА=2х
S треугольника ЕДА =(1/2)*ЕД*ДА=(1/2)*х*2х*cos30
(х^2)*(sqrt{3}/2)=2sqrt{3}
х=2
(1/2)АС=АЕ*cos30=4*(sqrt{3}/2)=2sqrt{3}
Т.к. угол ВАС делится на 3 равные части, то угол ВДА= углу ДАЕ= углу ЕАС=30.
Треугольник ВДА подобен ВАС по двум углам: ДВА=АВС, угол ВДА=ВАС=90 ,
=> угол ВСА= ДАВ=30
=>треугольник АЕС= равнобедренный , АЕ=АС
Треугольник ВДА= ЕДА по двум углам и стороне, ДА- общая, угол ВДА=ЕДА, угол ВАД=ЕАД.
=>ВД=ДЕ
обозначим ДЕ за х, тогда ВД=х, ЕС=2х, ЕА=2х
S треугольника ЕДА =(1/2)*ЕД*ДА=(1/2)*х*2х*cos30
(х^2)*(sqrt{3}/2)=2sqrt{3}
х=2
(1/2)АС=АЕ*cos30=4*(sqrt{3}/2)=2sqrt{3}
=> AC=4sqrt{3}
ВА=ВС*cos60=4x*(1/2)=4
S треугольника АВС =(1/2)*АВ*АС=8sqrt{3}
р (полупериметр)=6+2sqrt{3})
r=S/p
r=(8sqrt{3})/(6+2sqrt{3})=4sqrt{3}/(3+sqrt{3})=4/(1+sqrt{3})
S круга=п*r^2=(16п)/((1+sqrt{3})^2)=(8п)/(2+sqrt{3})=(8п)*(2-sqrt{3})
ВА=ВС*cos60=4x*(1/2)=4
S треугольника АВС =(1/2)*АВ*АС=8sqrt{3}
р (полупериметр)=6+2sqrt{3})
r=S/p
r=(8sqrt{3})/(6+2sqrt{3})=4sqrt{3}/(3+sqrt{3})=4/(1+sqrt{3})
S круга=п*r^2=(16п)/((1+sqrt{3})^2)=(8п)/(2+sqrt{3})=(8п)*(2-sqrt{3})
вот решение исправленное
Спасибо тебе большое.
пожалуйста =)
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад