Ответы
Ответ дал:
0
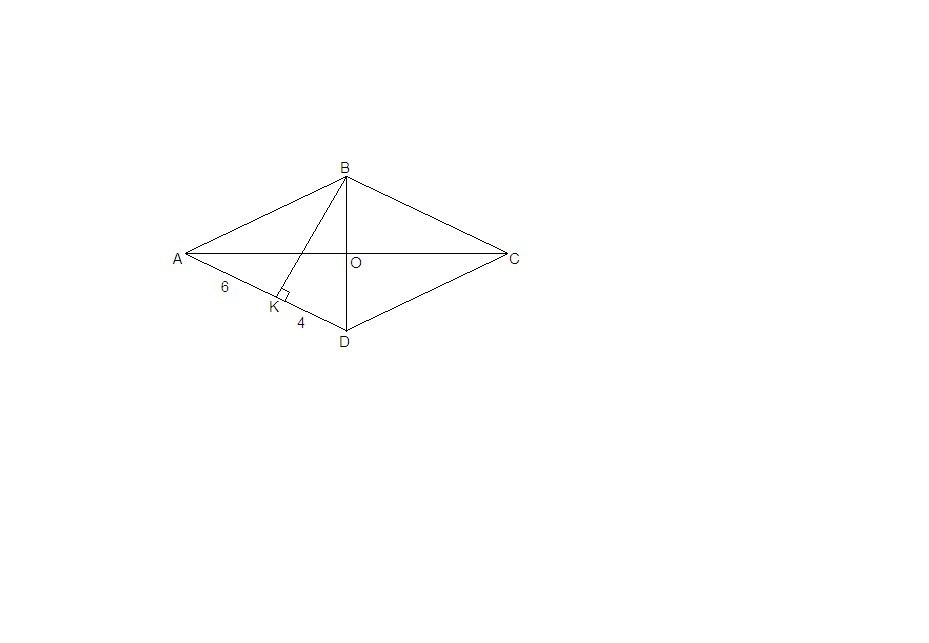
AD = AK + KD = 6 + 4 = 10 см - сторона ромба.
ΔАВК: ∠АКВ = 90°, АВ = 10 см, АК = 6 см, по теореме Пифагора
ВК = √(АВ² - АК²) = √(100 - 36) = √64 = 8 см
Sabcd = AD · BK = 10 · 8 = 80 см²
ΔBKD: ∠BKD = 90°, по теореме Пифагора
BD = √(BK² + KD²) = √(64 + 16) = √80 = 4√5 см
Sabcd = АС · BD/2
AC = 2·Sabcd /BD = 2·80/(4√5) = 40/√5 = 8√5 см
ΔАВК: ∠АКВ = 90°, АВ = 10 см, АК = 6 см, по теореме Пифагора
ВК = √(АВ² - АК²) = √(100 - 36) = √64 = 8 см
Sabcd = AD · BK = 10 · 8 = 80 см²
ΔBKD: ∠BKD = 90°, по теореме Пифагора
BD = √(BK² + KD²) = √(64 + 16) = √80 = 4√5 см
Sabcd = АС · BD/2
AC = 2·Sabcd /BD = 2·80/(4√5) = 40/√5 = 8√5 см
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад