Question

Помогите решить пожалуйста
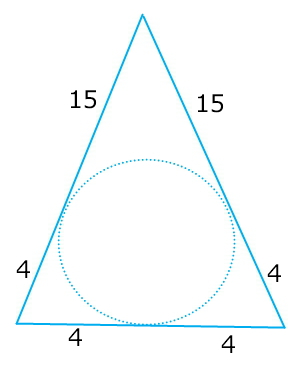
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Answer 1

отрезки касательных, проведенных из одной точки к окружности, РАВНЫ...
треугольник равнобедренный, значит две стороны известны по (15+4) = 19
основание = (4+4) = 8
Р = 19+19+8 = 46

Answer 2

Суть задачи в том, что стороны Δ - это касательные к окружности. Надо рассматривать части касательных ( от вершины до точки касания).Куски касательных, проведённых из одной точки равны между собой. То есть касательные из одной вершины равны по 15, из второй  4 и 4, из третьей 4 и 4.
Ответ Р = 46 (19+19+8)