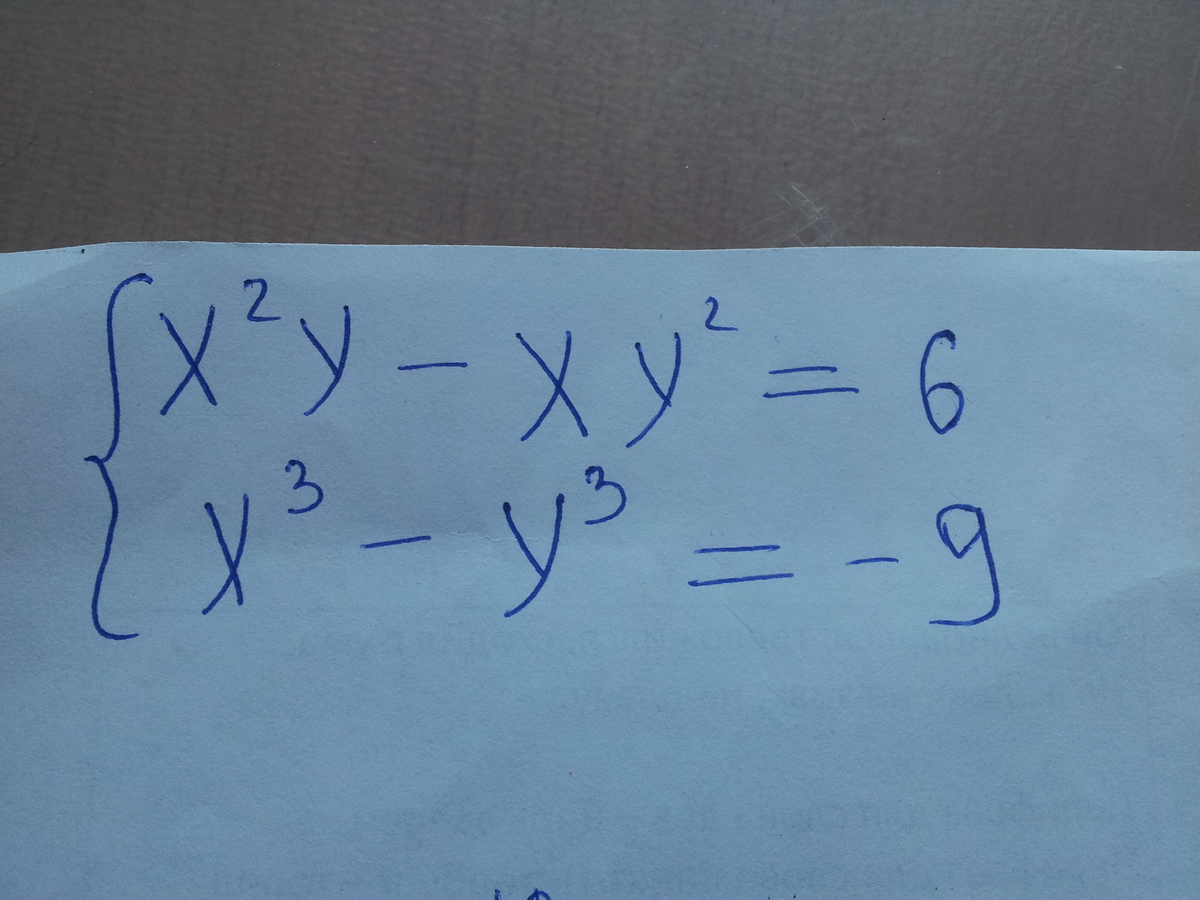Ответы
Ответ дал:
0
Выносим общий множитель
__________________________________
________________________________
Имеем 2 системы
Случай 1.
случай 2.
ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад