Question

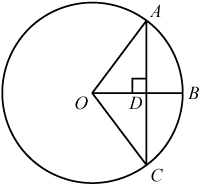
радиус OB окружности с центром в точке O пересекает хорду AC в точке D и перпендикулярен ей найдите длину хорды AC если BD = 2 см, а радиус окружности равен 5 см.

Помогите очень нужно

Answer 1

Продлив радиус ВО до пересечения с окружностью точке М. получим две пересекающиеся хорды: АС и ВМ (. диаметр ) 
Длина DM=2r-2= 8 см 
Произведения отрезков пересекающихся хорд равны. 
Так как радиус пересекает хорду АС под прямым углом, АD=DC.
Тогда АD*DC=AC²
АD²=2×8=16 см²
АD=√16=4 см
AC=2×AD=8 см