Ответы
Ответ дал:
1
решение в приложении:
Приложения:
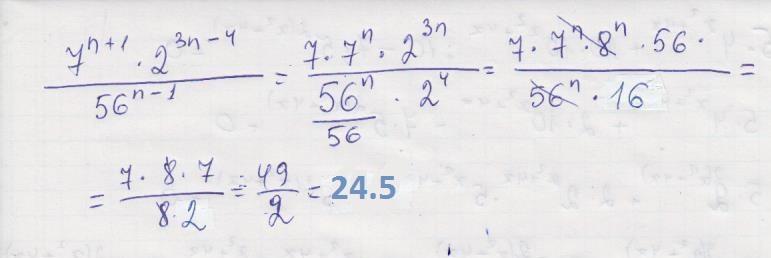
ndusha:
2^4=16
спасибо исправила!
:-)
не, там старый рисунок остался
исправила, все проверила
Ответ дал:
1
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад