Question

расстояние между серединами 2 перпендикулярных хорд окружности равно 8 см. Найдите расстояние от центра окружности до точки перессечения хорд

Answer 1

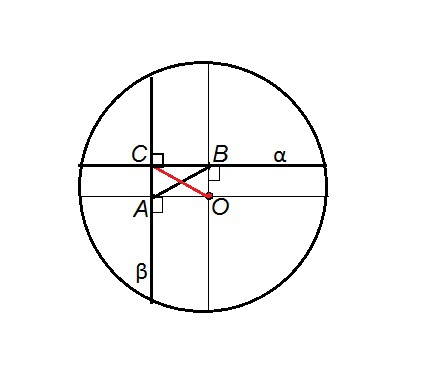
Пусть даны хорды  α  и β
Обозначим середину хорды  α буквой В, середину хорды β буквой А.
АВ - расстояние между центрами хорд и равно 8 см.
Из центра О окружности проведем к А и В радиусы. 
Радиус окружности, проведенный в середину хорды, перпендикулярен ей. 
Тогда углы ОВС и ОАС -прямые, а четырехугольник АСВО - прямоугольник. Диагонали прямоугольника равны. 
ОС - расстояние от центра окружности до точки пересечения хорд - диагональ прямоугольника АСВО.
 ОС=АВ=8 см - искомое расстояние.