Даю 165 баллов. На полпути затруднения, может у меня ошибка. В общем, спасайте
Приложения:
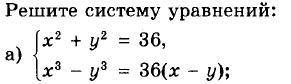
Аноним:
Спамеры пришли блин
Ответы
Ответ дал:
1
Разложим второе уравнение на множители

Разбивается на 2 системы
Первая система
***************************************

Пусть u=x+y, v=xy, получаем

Решив систему

Возвращаемся к замене


******************************************
Вторая система

Ответ:
Разбивается на 2 системы
Первая система
***************************************
Пусть u=x+y, v=xy, получаем
Решив систему
Возвращаемся к замене
******************************************
Вторая система
Ответ:
а 0 и плюс минус 6 точно будут? в ответах указано лишь про 3 корень из 2
Сейчас подстановкой проверю
Да, будут. В ответе то наверное не полностью они решили
хорошо, спасибо огромное) теперь буду разбираться и подобным образом оставльные решать)
На здоровье!
А первые 4 рзве подходят? Во второй системе их подставь и проверь!
разве*
Какие корни?
Спасибо за лучший.
это тебе спасибо за помощь)
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад