2.1-составить уравнение касательной и нормали к заданной к кривым в точке с абсциссой х0.
3.1-найти производные dy/dx для функций,заданных в параметрическом виде
Приложения:

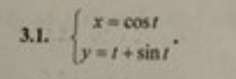
Ответы
Ответ дал:
1
2.1)
а) 1. Найдем производную функции:

2. Найдем значение производной в точке х0:

3. Запишем уравнение касательной:



4. Уравнение нормали:


б)
![y= \sqrt[3]{-3x^{2}-15} y= \sqrt[3]{-3x^{2}-15}](https://tex.z-dn.net/?f=y%3D+%5Csqrt%5B3%5D%7B-3x%5E%7B2%7D-15%7D)
![y'(x)=(\sqrt[3]{-3x^{2}-15})'=-\frac{2x}{\sqrt[3]{(-3x^{2}-15})^{2}} y'(x)=(\sqrt[3]{-3x^{2}-15})'=-\frac{2x}{\sqrt[3]{(-3x^{2}-15})^{2}}](https://tex.z-dn.net/?f=y%27%28x%29%3D%28%5Csqrt%5B3%5D%7B-3x%5E%7B2%7D-15%7D%29%27%3D-%5Cfrac%7B2x%7D%7B%5Csqrt%5B3%5D%7B%28-3x%5E%7B2%7D-15%7D%29%5E%7B2%7D%7D)
![y'(x_{0})=y'(2)=-\frac{2*2}{\sqrt[3]{(-3*2^{2}-15})^{2}}=-\frac{4}{\sqrt[3]{(-27})^{2}}=-\frac{4}{\sqrt[3]{3^{6}}}=-\frac{4}{9} y'(x_{0})=y'(2)=-\frac{2*2}{\sqrt[3]{(-3*2^{2}-15})^{2}}=-\frac{4}{\sqrt[3]{(-27})^{2}}=-\frac{4}{\sqrt[3]{3^{6}}}=-\frac{4}{9}](https://tex.z-dn.net/?f=y%27%28x_%7B0%7D%29%3Dy%27%282%29%3D-%5Cfrac%7B2%2A2%7D%7B%5Csqrt%5B3%5D%7B%28-3%2A2%5E%7B2%7D-15%7D%29%5E%7B2%7D%7D%3D-%5Cfrac%7B4%7D%7B%5Csqrt%5B3%5D%7B%28-27%7D%29%5E%7B2%7D%7D%3D-%5Cfrac%7B4%7D%7B%5Csqrt%5B3%5D%7B3%5E%7B6%7D%7D%7D%3D-%5Cfrac%7B4%7D%7B9%7D)
![y(x_{0})=y(2)=\sqrt[3]{-3*4-15}=\sqrt[3]{-27}=-3 y(x_{0})=y(2)=\sqrt[3]{-3*4-15}=\sqrt[3]{-27}=-3](https://tex.z-dn.net/?f=y%28x_%7B0%7D%29%3Dy%282%29%3D%5Csqrt%5B3%5D%7B-3%2A4-15%7D%3D%5Csqrt%5B3%5D%7B-27%7D%3D-3)


3.1)
1. Найдем дифференциалы обеих частей каждого из равенств:

2. Разделим второе уравнение на первое:

Это и есть первая производная от функции, заданной параметрически.
3. Для нахождения второй производной необходимо выполнить преобразования:

а) 1. Найдем производную функции:
2. Найдем значение производной в точке х0:
3. Запишем уравнение касательной:
4. Уравнение нормали:
б)
3.1)
1. Найдем дифференциалы обеих частей каждого из равенств:
2. Разделим второе уравнение на первое:
Это и есть первая производная от функции, заданной параметрически.
3. Для нахождения второй производной необходимо выполнить преобразования:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад