Question

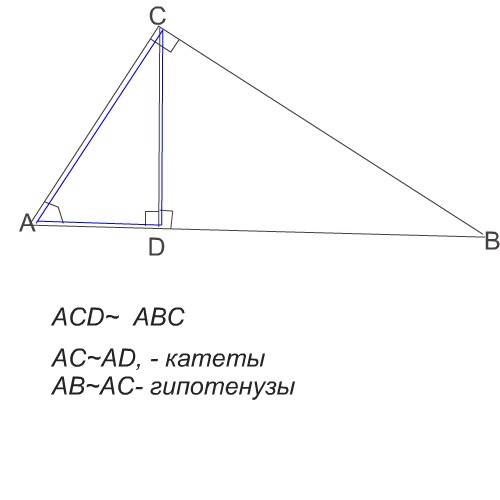
Дан прямоугольный треугольник ABC, угол C=90 градусов, из него проведен перпендикуляр к стороне AB=9 см(они пересекаются в точке D). AD=4 см.

Найти AC, доказать, что треугольник ABC подобен треугольнику ACD.

Решить через пропорцию.

Answer 1

АВ делится на отрезки АД=4см и ВД=5см

Высота, опущенная к гипотенузе находится по формуле СД=корень квадратный из произведения АД на ВД

СД=корень квадратный из 4*5=20. Знаем два катета в треугольнике АСД, находим гипотенузу. АС2=СД2+АД2=20+16=36  АС=6

 

Подобие треугольников по двум углам: угол ВАС=ДАС (общий для двух треугольников), угол ВАС=углуАДС=90град 

Answer 2

·Треугольники АСD и АВС подобны.

Оба прямоугольные,

угол А - общий.

 

Если в прямоугольных треугольниках один из острых углов одного треугольника равен острому углу другого, то они подобны.

катеты АС~AD, гипотенузы AB~AC

АС:4=АВ:АС

АС²=4·9

АС²=36

АС=6 cм