В основание пирамиды лежит равнобедренный треугольник с углом альфа при основании, а все боковые ребра пирамиды образуют с плоскостью основания угол бета.
tolya91:
что надо найти то?
найти объем пирамиды, если боковая сторона основания пирамиды равна b. Не дописала
Ответы
Ответ дал:
3
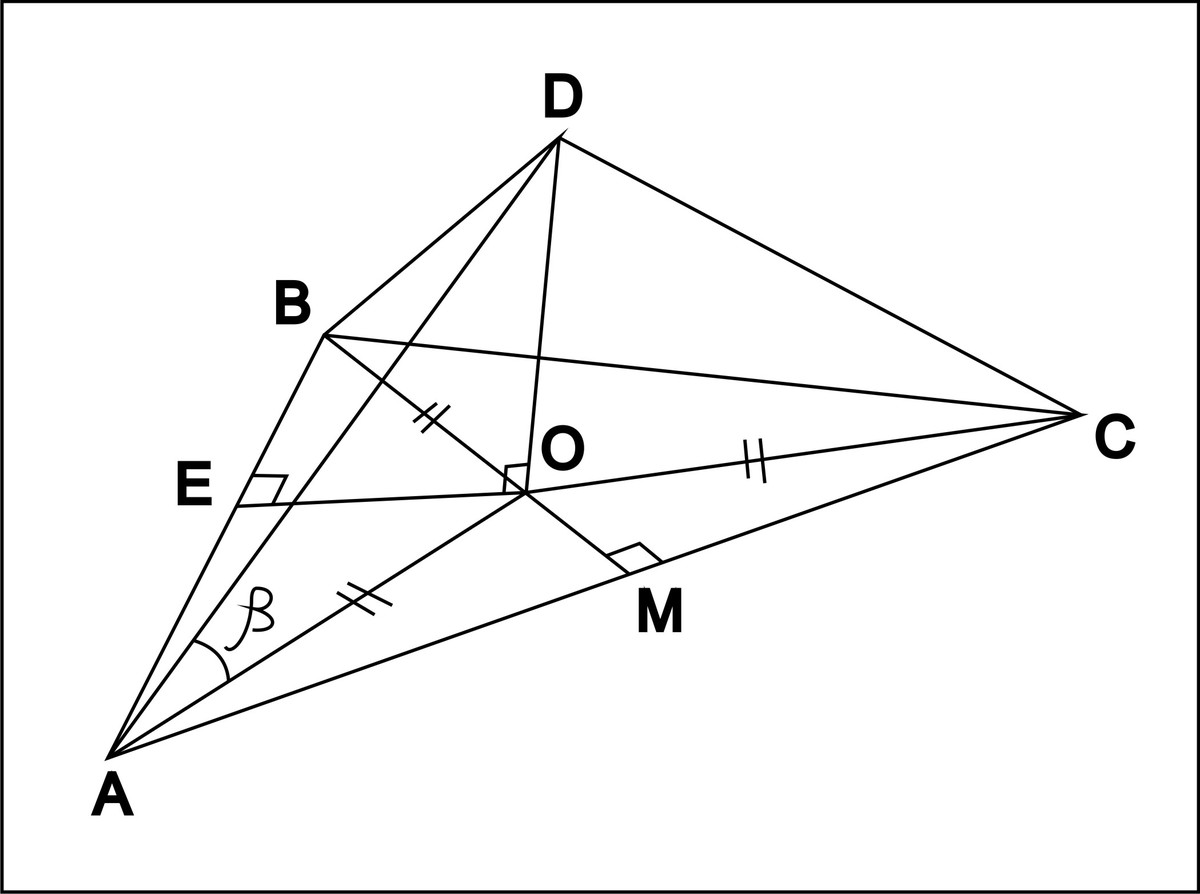
угол ВАС= альфа
по скольку углы между боковыми сторонами и основанием равны, то боковые стороны тоже равны и их проекции тоже равны
АО=ОВ=ОС
опустим перпендикуляры из О на АВ и на АС
треугольник ВОЕ подобен ВАМ
АВ/ВО=ВМ/ЕВ
b/BO=(bsinальфа)/(b/2)
BO=b/(2sinальфа)
tgбетта=DO/BO
DO=tgбетта*AO=(tgбетта*b)/(2sinальфа)
S(основания)=АМ*МВ= bsinальфа*bcosальфа
Объём пирамиды 1/3 высоты на площадь основания
V(пирамиды)=(1/3)HS=(1/6)*tgбетта*b^3*cosальфа
по скольку углы между боковыми сторонами и основанием равны, то боковые стороны тоже равны и их проекции тоже равны
АО=ОВ=ОС
опустим перпендикуляры из О на АВ и на АС
треугольник ВОЕ подобен ВАМ
АВ/ВО=ВМ/ЕВ
b/BO=(bsinальфа)/(b/2)
BO=b/(2sinальфа)
tgбетта=DO/BO
DO=tgбетта*AO=(tgбетта*b)/(2sinальфа)
S(основания)=АМ*МВ= bsinальфа*bcosальфа
Объём пирамиды 1/3 высоты на площадь основания
V(пирамиды)=(1/3)HS=(1/6)*tgбетта*b^3*cosальфа
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад