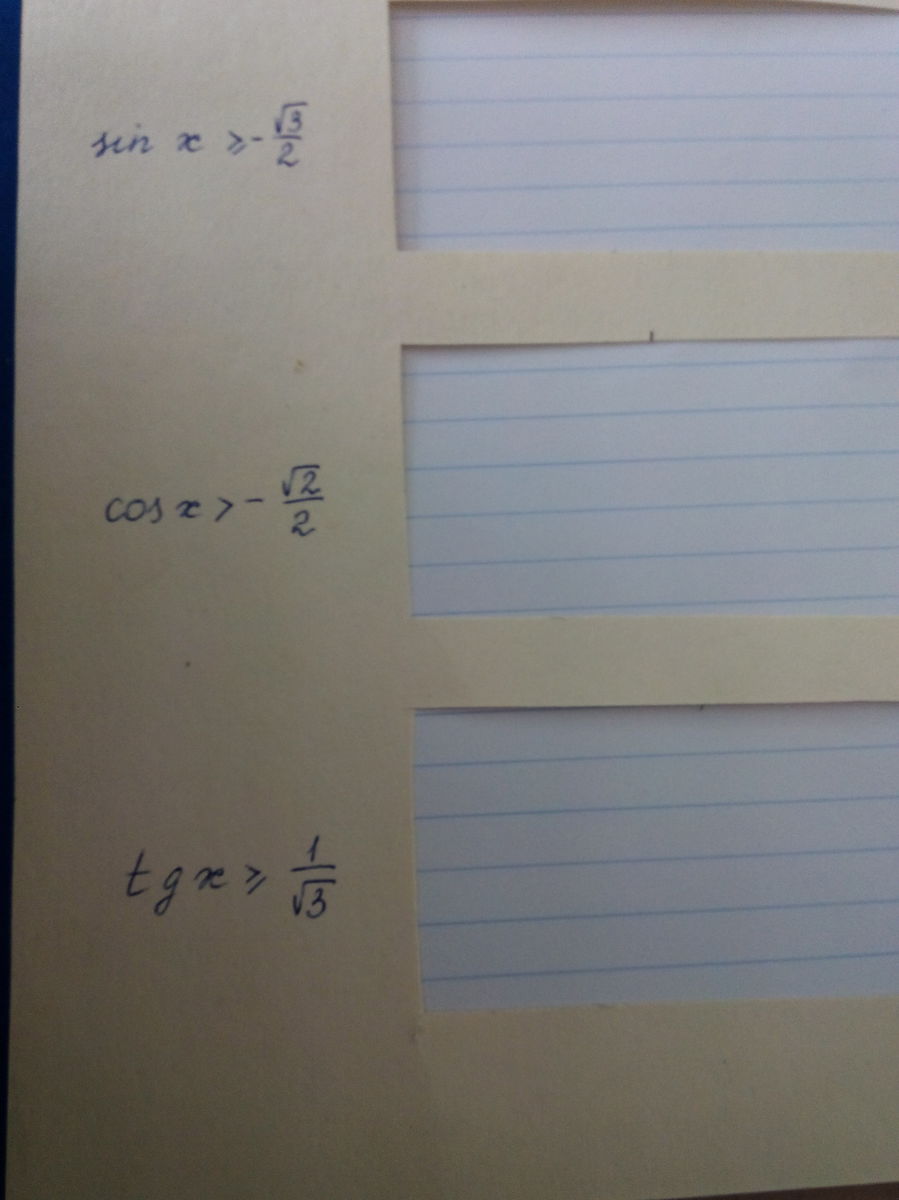Ответы
Ответ дал:
1
1) sinx ≥ -√3/2 .
Неравенство удобно решить сначала на отрезке [ -π/2 ; 3π/2] .
x∈ [ -π/3 +2π*k ; π+π/3 +2πk ] ,k∈ Z.
x∈ [ -π/3 +2π*k ; 4π/3 +2πk ] ,k∈ Z.
2) cosx > - √2/2 ;
Неравенство удобно решить сначала на отрезке [ -π ;π] .
- π+π/4 < x < π-π/4;
-3π/4 < x < 3π/4;
x∈( -3π/4 +2π*k ;3π/4 +2π*k ) , k∈Z.
3) tqx ≥1/√3 .
Неравенство удобно решить сначала на интервале ( -π/2 ; π/2) .
π /6 ≤ x <π/2 ;
x ∈(π /6 +π*k ;π/2 +π*k) ,k∈ Z.
=======================================================
!!! Удобно использовать(наглядные) графические представления.
Неравенство удобно решить сначала на отрезке [ -π/2 ; 3π/2] .
x∈ [ -π/3 +2π*k ; π+π/3 +2πk ] ,k∈ Z.
x∈ [ -π/3 +2π*k ; 4π/3 +2πk ] ,k∈ Z.
2) cosx > - √2/2 ;
Неравенство удобно решить сначала на отрезке [ -π ;π] .
- π+π/4 < x < π-π/4;
-3π/4 < x < 3π/4;
x∈( -3π/4 +2π*k ;3π/4 +2π*k ) , k∈Z.
3) tqx ≥1/√3 .
Неравенство удобно решить сначала на интервале ( -π/2 ; π/2) .
π /6 ≤ x <π/2 ;
x ∈(π /6 +π*k ;π/2 +π*k) ,k∈ Z.
=======================================================
!!! Удобно использовать(наглядные) графические представления.
можете помочь мне с еще 1 заданием по алгебре?
да
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад