130 баллов!!!ССЮЮЮЮДАААРешите 4 логарифмических неравенства,надо знать,как они решаются,с меня лучший ответ.
Приложения:
Kulakca:
постараюсь объяснить на уровне 9 класса сейчас. Если это нужно
Я чуток знакома с материалом.Всё,что я знаю,как они читаются и их математический смысл(логарифм-число показателя,в котором основание даёт число).Не очень хорошо.Если вам несложно,можете немного объяснить прямо в решение.Спасибо!:)
Я по частям буду выкладывать
Всё просто, всё сводится к методу интервалов в конечном итоге.
Пока всё понятно?
ВСЁ ОЧЕНЬ ПОНЯТНО:))
Уважаемые, пишите в ЛС, получите от этого еще предупреждение.
Да, я иногда грешил этим. Но собеседника просто иногда было не остановить ;)
Пойду выше.Не могу выразиться о понятости мной решения?
не понимаю Вас немного ;)
Ответы
Ответ дал:
2
3
Сделаем замену 2^x = t, t > 0 - показательная функция принимает только положительные значения, что мы и будем учитывать в дальнейшем.
Тогда 2^(1-x) = 2/2^x = 2/t
Неравенство с учётом замены приобретает вид:
t + 2/t - 3 < 0
Можем умножить обе части неравенства на t > 0. При этом знак неравенства не меняем:
t^2 -3t + 2 < 0
Решаем квадратичное неравенство методом интервалов:
(t - 2)(t-1) < 0
Отсюда 1< t < 2
Ну здесь всё хорошо вроде бы: условие t > 0 выполняется
Теперь вспоминаем, кто такой t:
1 < 2^x < 2
До сего момента специфики было не очень много. Сделали замену(в этом ничего нового нет). Теперь решать будем показательное неравенство. Для этого приведём все степени к удобному для нас основанию(то есть. к 2)
2^0 < 2^x < 2^1
2^x - возрастающая функция, поэтому
0 < x < 1
4
При решении показательных неравенств приходится во многих случаях приводить все степени к одному основанию. В этом неравенстве у нас два "несовместимых" основания: 2 и 5. Значит. эта идея тут не сработает.
Но зато я знаю, что 5^x > 0 - показательная функция принимает лишь положительные значения. Поэтому я спокойно смогу разделить обе части неравенства на 5^x. Но перед этим немного преобразую левую часть:
4 * 2^x - 8 * 2^x - 16 * 2^x > 5 * 5^x - 5^x
Здесь я воспользовался свойствами степеней. Например, 2^(x+2) = 2^x * 2^2 = 4*2^x.
далее:
-20 * 2^x > 4 * 5^x
-5 * 2^x > 5^x
Теперь делим на 5^x > 0:
-5 * (2/5)^x > 1
Ну и сделали то, что хотели - пришли к одному основанию.
(2/5)^x < -1/5
И теперь мы видим одну важную вещь. Слева - показательная функция, которая принимает лишь положительные значения. Из нашего неравенства видно, что она меньше отрицательного значения, чего быть не может. Значит, решений у неравенства нет.
Сделаем замену 2^x = t, t > 0 - показательная функция принимает только положительные значения, что мы и будем учитывать в дальнейшем.
Тогда 2^(1-x) = 2/2^x = 2/t
Неравенство с учётом замены приобретает вид:
t + 2/t - 3 < 0
Можем умножить обе части неравенства на t > 0. При этом знак неравенства не меняем:
t^2 -3t + 2 < 0
Решаем квадратичное неравенство методом интервалов:
(t - 2)(t-1) < 0
Отсюда 1< t < 2
Ну здесь всё хорошо вроде бы: условие t > 0 выполняется
Теперь вспоминаем, кто такой t:
1 < 2^x < 2
До сего момента специфики было не очень много. Сделали замену(в этом ничего нового нет). Теперь решать будем показательное неравенство. Для этого приведём все степени к удобному для нас основанию(то есть. к 2)
2^0 < 2^x < 2^1
2^x - возрастающая функция, поэтому
0 < x < 1
4
При решении показательных неравенств приходится во многих случаях приводить все степени к одному основанию. В этом неравенстве у нас два "несовместимых" основания: 2 и 5. Значит. эта идея тут не сработает.
Но зато я знаю, что 5^x > 0 - показательная функция принимает лишь положительные значения. Поэтому я спокойно смогу разделить обе части неравенства на 5^x. Но перед этим немного преобразую левую часть:
4 * 2^x - 8 * 2^x - 16 * 2^x > 5 * 5^x - 5^x
Здесь я воспользовался свойствами степеней. Например, 2^(x+2) = 2^x * 2^2 = 4*2^x.
далее:
-20 * 2^x > 4 * 5^x
-5 * 2^x > 5^x
Теперь делим на 5^x > 0:
-5 * (2/5)^x > 1
Ну и сделали то, что хотели - пришли к одному основанию.
(2/5)^x < -1/5
И теперь мы видим одну важную вещь. Слева - показательная функция, которая принимает лишь положительные значения. Из нашего неравенства видно, что она меньше отрицательного значения, чего быть не может. Значит, решений у неравенства нет.
Ага,как всё доступно,ясно изложено!А всё-таки несложно.Это 11 класс?Теперь я что-то знаю.Буду ежедневно пересматривать ваше решение.У меня уже голова не работает,честно говоря.Но изложили гениально.Буду учиться на вашем примере сама.БОЛЬШОЕ СПАСИБО!
а Вам не нужны остальные неравенства? ;)
Если хотите, когда-нибудь напишите мне, и я объясню показательные неравенства ;)
решения есть ниже,а честно говоря,я на просторах их нашла,решила двгиаться с алгеброй дальше,у самой ГИА впереди,хочу здесь решать старшеклассникам логарифмы,тригонометрические почти научилась решать:) спасибо,я буду платить баллами)
да я и так готов помочь ;)
а что, так сильно нравится математика, что далеко продвинулись? ;)
слушайте, напишите в ЛС
здесь просто немного не место. Если есть вопросы, напишите туда, я подскажу что-нибудь
просто нас забанить могут за такие проделки ;)
Если вопросы есть, как написать туда, нажимаете на мою аватарку, заходите в мой профиль, там ссылочка есть "написать сообщение"
Ответ дал:
0
*****************************************
Приложения:
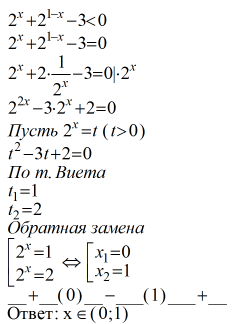
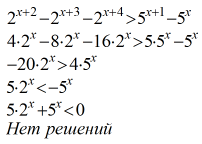
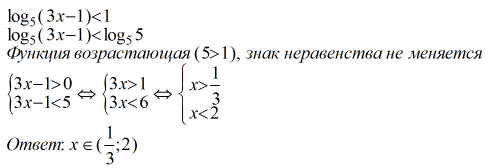
Есть ошибка
Сейчас испрвлю
Большое спасибо,жду
Изменил
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад