Найдите все значения параметра а, при каждом из которых следующая система уравнений имеет хотя бы одно решение.
Приложения:
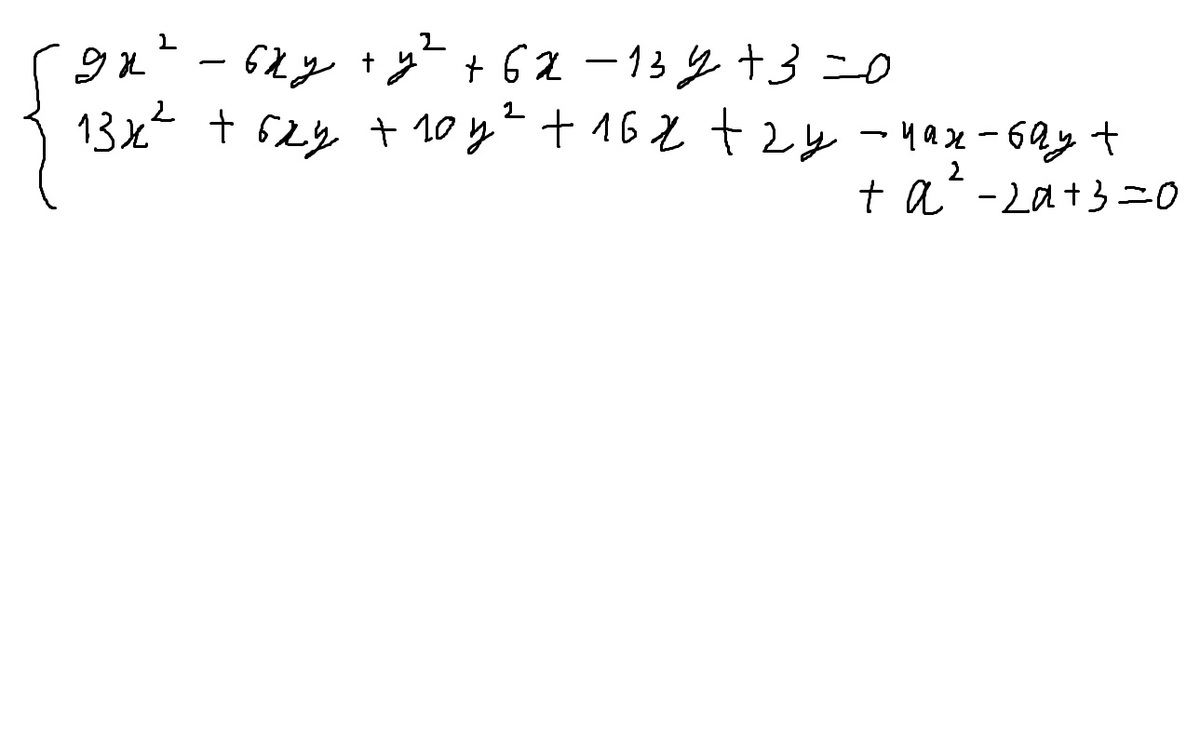
Матов:
перезагрузи страницу если не видно
Ответы
Ответ дал:
2
Отнимаем одно уравнение от другого  Получили квадратное уравнение
Получили квадратное уравнение ![b^2+(5-2a)b+a^2-2a=0\\ D \geq 0\\ D=(5-2a)^2-4*(a^2-2a) \geq 0 \\ a \in (-\infty; \frac{25}{2}] b^2+(5-2a)b+a^2-2a=0\\ D \geq 0\\ D=(5-2a)^2-4*(a^2-2a) \geq 0 \\ a \in (-\infty; \frac{25}{2}]](https://tex.z-dn.net/?f=+b%5E2%2B%285-2a%29b%2Ba%5E2-2a%3D0%5C%5C+D+%5Cgeq+0%5C%5C+D%3D%285-2a%29%5E2-4%2A%28a%5E2-2a%29+%5Cgeq+0+%5C%5C+a+%5Cin+%28-%5Cinfty%3B+%5Cfrac%7B25%7D%7B2%7D%5D)
Рассмотрим любую из прямых вторую можно не рассматривать , так как они симметричны относительно друг - друга
вторую можно не рассматривать , так как они симметричны относительно друг - друга  выразив со второе и с первой
выразив со второе и с первой 
 первое , уравнение параболы , которая
первое , уравнение параболы , которая  , второе уравнение прямой , то есть необходимое условие для первой пары системы равенств , такое нужно чтобы , прямая была касательная к параболе
, второе уравнение прямой , то есть необходимое условие для первой пары системы равенств , такое нужно чтобы , прямая была касательная к параболе

подставляя найденные значения в
Получаем
 , значит все решения идут между этими числами .
, значит все решения идут между этими числами .
2.Теперь со вторым , это фигура второго порядка Эллипс , так как мы выяснили что , значит для данной фигуры, при любых значениях выше сказанная прямая будет пересекать.
, значит для данной фигуры, при любых значениях выше сказанная прямая будет пересекать.
![a \in [\frac{2-3\sqrt{2}}{3}; \frac{2+3\sqrt{2}}{3}] a \in [\frac{2-3\sqrt{2}}{3}; \frac{2+3\sqrt{2}}{3}]](https://tex.z-dn.net/?f=++++a+%5Cin+%5B%5Cfrac%7B2-3%5Csqrt%7B2%7D%7D%7B3%7D%3B+%5Cfrac%7B2%2B3%5Csqrt%7B2%7D%7D%7B3%7D%5D)
Рассмотрим любую из прямых
подставляя найденные значения в
Получаем
2.Теперь со вторым , это фигура второго порядка Эллипс , так как мы выяснили что
С ответом не совпадает((
подождите я его не закончил , само отправилось что то
Сразу скажу, что решение принимаю. Но предполагалось решать несколько иначе
Без использования геометрических интерпретаций
Я извиняюсь, что позабыл написать про это.
Впрочем, я уже решил эту задачу!
Большое спасибо за другой способ решения. Будет, с чем сравнивать ;)
никаких геометрических интерпретаций здесь особа не наблюдается , если вы про упомянутый на строку "Эллипс" то он тут ради того чтобы пояснить почему именно данный отрезок [2-3√2/3 3√2+2/3] принадлежит решению , существование другого решения скажем так " не геометрического" я не отрицаю .
Не за что !
Не за что !
Извините, я просто не знакомился глубоко ещё с Вашим решением. Сейчас познакомлюсь, тогда смогу сказать определённо
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад