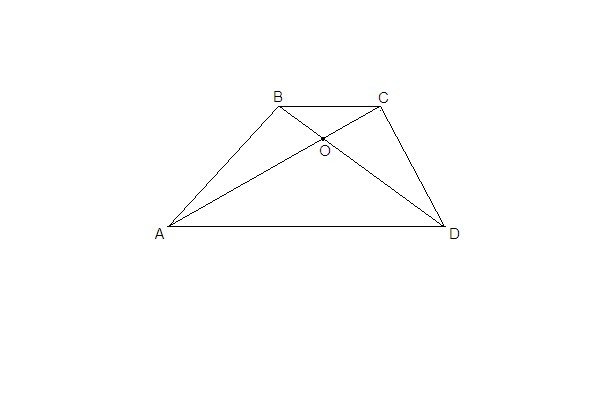
В трапеции ABCD диагонали AC и BD пересекаются в точке O, AO:CO=3:1. При средней линии трапеции, равной 24, найдите ее основания.
Ответы
Ответ дал:
0
ΔAOD подобен ΔСОВ по двум углам (углы при вершине О равны как вертикальные, ∠OAD = ∠OCB как накрест лежащие при пересечении AD║BC секущей АС)
AD/BC = AO/OC = 3/1 ⇒ AD = 3BC
Средняя линия трапеции равна полусумме оснований:
(AD + BC)/2 = 24
AD + BC = 48
4BC = 48
BC = 12
AD = 3BC = 36
AD/BC = AO/OC = 3/1 ⇒ AD = 3BC
Средняя линия трапеции равна полусумме оснований:
(AD + BC)/2 = 24
AD + BC = 48
4BC = 48
BC = 12
AD = 3BC = 36
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад