шар радиуса R вписан в конус из центра шара образующая конуса видно под углом альфа. Найти объём конуса
Ответы
Ответ дал:
2
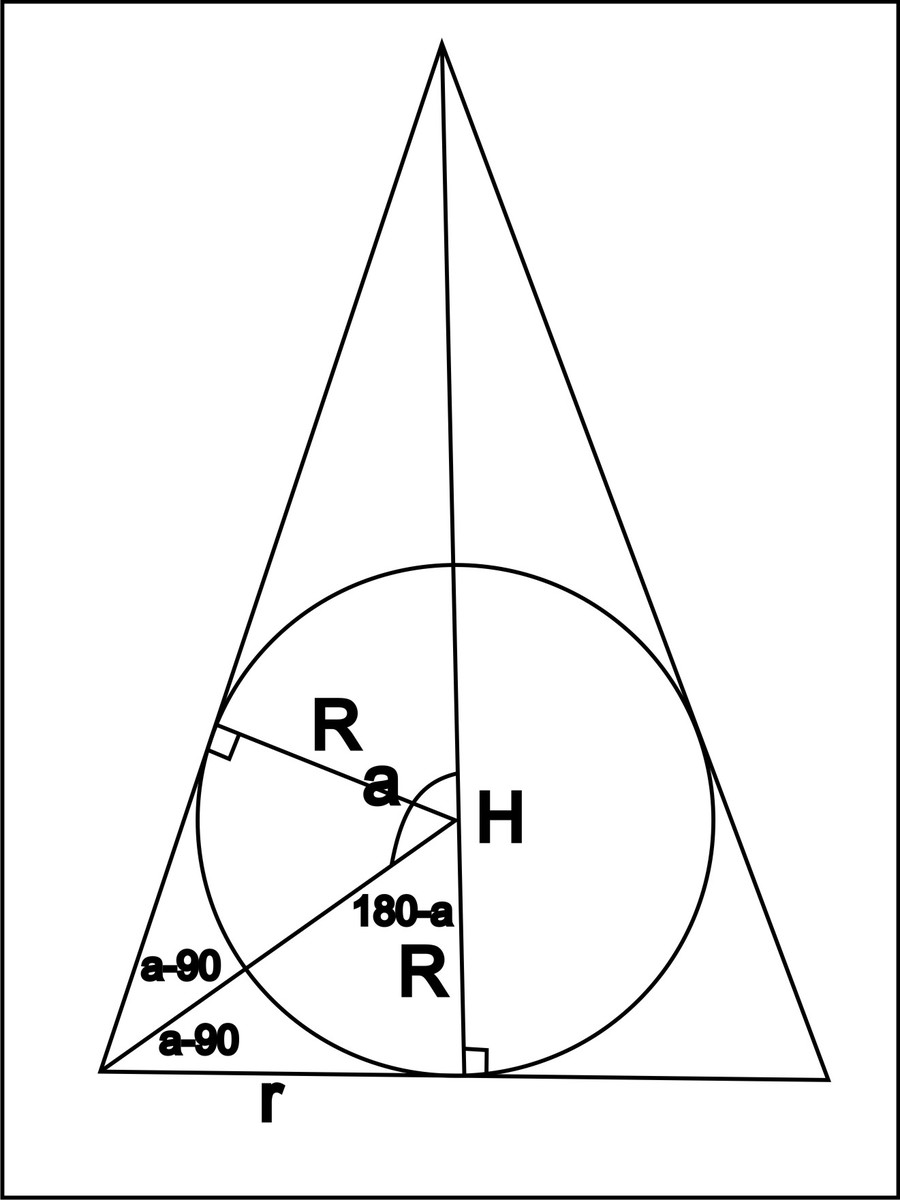
на рисунке осевое сечение конуса
r-радиус основания конуса
a-aльфа
H-высота конуса
r/R=tg(180-a)
tg(180-a)=-tga
r=-tga*R
H/r=tg(2a-180)
tg(2a-180)=tg(2a)
H=r*tg(2a)=-tga*R*tg(2a)
V=(1/3)*пr^2*H=-(1/3)п*tg^3(a)*R^3*tg(2a)
r-радиус основания конуса
a-aльфа
H-высота конуса
r/R=tg(180-a)
tg(180-a)=-tga
r=-tga*R
H/r=tg(2a-180)
tg(2a-180)=tg(2a)
H=r*tg(2a)=-tga*R*tg(2a)
V=(1/3)*пr^2*H=-(1/3)п*tg^3(a)*R^3*tg(2a)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад