Question

В прямоугольном треугольнике АВС С=90 градусов АВ=10 см угол АВС=30 градусов С центром в точке А проведена окружность. Каким должен быть радиус этой окружности чтобы 1.Окружность касалась прямой ВС 2.Не имела с ней общих точек.3.Имела с ней 2 общие точки.

Answer 1

Катет АС противолежит углу 30° и равен половине гипотенузы АВ. 

АС=5 см. 

Окружность и прямая могут касаться и иметь одну общую точку, не касаться и не иметь общих точек, или пересекаться, при этом они будут иметь  две общие точки . 

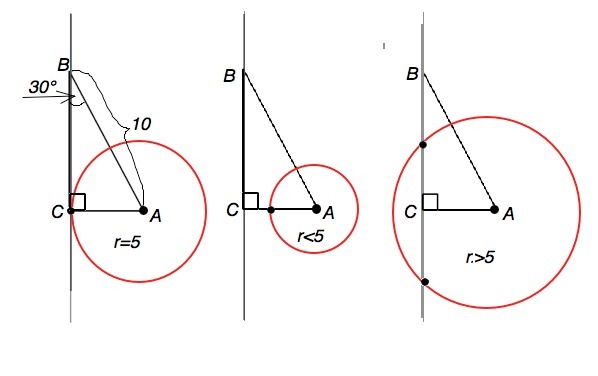
1) радиус, проведенный в точку касания, равен катету r=АС =5 см( т.к. угол ВСА=90°, а радиус перпендикулярен касательной в точке касания)

2) Окружность не будет касаться прямой ВС, если её радиус меньше катета АС. r < AC; r < 5 см

3) Окружность и прямая пересекутся, если радиус больше расстояния от центра окружности до прямой. r > AC' r > 5 см