Question

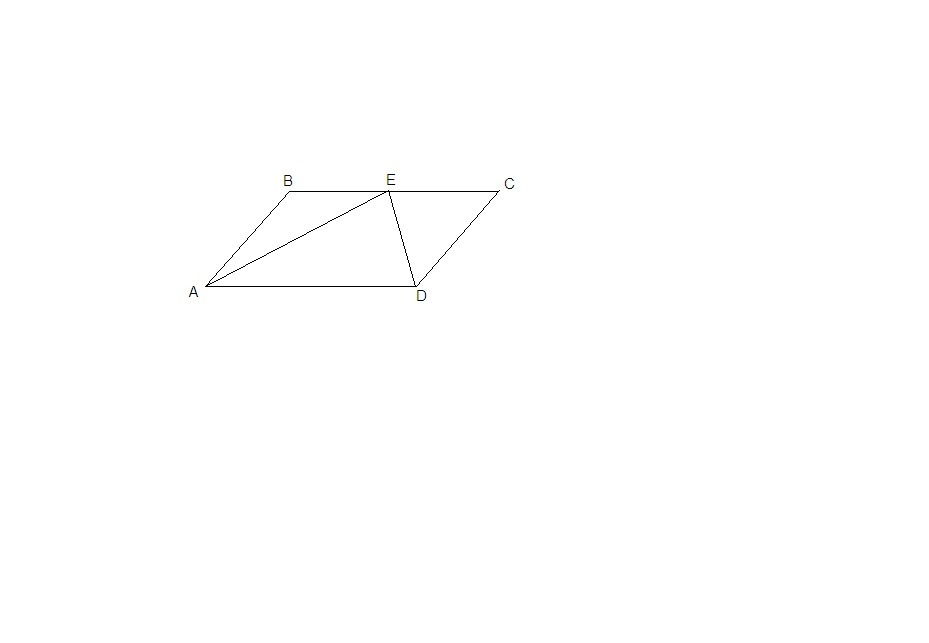
Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке Е стороны ВС. Докажите, что Е - середина ВС.

Answer 1

∠BEA = ∠EAD как накрест лежащие при пересечении BC║AD секущей АЕ,
∠EAD = ∠ЕАВ т.к. АЕ биссектриса, значит,
∠BEA = ∠ЕАВ ⇒ ΔЕАВ равнобедренный.
АВ = ВЕ

∠DEC = ∠EDA как накрест лежащие при пересечении BC║AD секущей DЕ,
∠EDA = ∠ЕDC т.к. DЕ биссектриса, значит,
∠DEC = ∠ЕDC ⇒ ΔЕDC равнобедренный.
CD = CE

АВ = ВЕ
CD = CE, AB = CD ⇒ BE = CE. ⇒ Е - середина ВС